簡介
線性時不變系統
英文：linear time invariant（LTI）
它包括連續時間系統與離散時間系統
概念
線性系統有兩種定義：
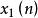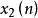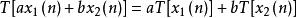線性時不變系統
線性時不變系統
線性時不變系統
線性時不變系統
線性時不變系統(1) 根據系統的輸入和輸出關係是否具有線性來定義 滿足疊加原理的系統具有線性特性。即若對兩個激勵 和 ，有 ，式中 、 為任意常數。不滿足上述關係的為非線性系統。
(2) 根據組成系統的元件特性來定義 由線性元件和獨立電源組成的系統。
系統性質
時不變系統
時不變系統：就是系統的參數不隨時間而變化，即不管輸入信號作用的時間先後，輸出信號回響的形狀均相同，僅是從出現的時間不同。用數學表示為T[x(n)]=y[n]則 T[x(n-n0)]=y[n-n0]，這說明序列x(n)先移位後進行變換與它先進行變換後再移位是等效的。
線性時不變系統
線性時不變系統：既滿足疊加原理又具有時不變特性，它可以用單位脈衝回響來表示。單位脈衝回響是輸入端為單位脈衝序列時的系統輸出，一般表示為h(n)，即h(n)=T[δ(n)]。
任一輸入序列x(n)的回響y(n)=T[x(n)]=T[ δ(n-k)]；
由於系統是線性的，所以上式可以寫成y(n)=T[δ(n-k)]；
又由於系統是時不變的，即有T[δ(n-k)]=h(n-k)；
從而得y(n)=h(n-k)=x(n)*h(n)；
這個公式稱為線性卷積，用“*”表示。
線性時不變系統
齊次性
若激勵f(t)產生的回響為y(t)，則激勵Af(t)產生的回響即為Ay(t)，此性質即為齊次性。其中A為任意常數。
f(t)系統y(t)，Af(t)系統Ay(t)
疊加性
若激勵f1(t)與f2(t)產生的回響分別為y1(t)， y2(t)，則激勵f1(t)+f2(t)產生的響
應即為y1(t)+y2(t)，此性質稱為疊加性。
線性
若激勵f1(t)與f2(t)產生的回響分別為y1(t)， y2(t)，則激勵A1f1(t)+A2f2(t)產生
的回響即為A1y1(t)+A2y2(t)，此性質稱為線性。
時不變性
若激勵f(t)產生的回響為y(t)，則激勵f(t-t0)產生的回響即為y(t-t0)，此性質稱為
不變性，也稱定常性或延遲性。它說明，當激勵f(t)延遲時間t0時，其回響y(t)也延
遲時間t0，且波形不變。
微分性
若激勵f(t)產生的回響為y(t)，則激勵f'(t)產生的回響即y’(t),此性質即為微分性。
積分性
若激勵f(t)產生的回響為y(t)，則激勵f(t)的積分產生的回響即為y(t)的積分。此性質稱為積分性。
