定義
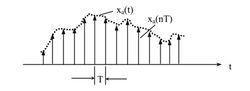圖1因為現實世界裡存在的是模擬信號，因此數位訊號處理的第一個問題是將信號離散化（取樣） ，然後進行量化編碼，最後進行數字處理。將連續信號變成離散信號的常用方法是等間隔或不等間隔周期取樣，如下圖1：
表示為圖2：
其中 T 稱為取樣周期，T 的倒數 T f s / 1 = 稱為取樣頻率或取樣率。只要取樣 T 足夠小，可用取樣值來描述任一連續函式。當取樣間距小到 0，則取樣函式與被取樣函式密不可分，當取樣間隔不為 0，只要根據斯特採樣定理即可保證任意模擬信號能由它的採樣信號恢復。
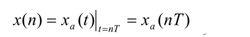圖2取樣定理 —— Nyquist 定理
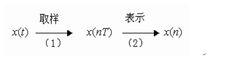圖3任一帶限函式（f<B）能嚴格由它取樣值確定，只要均勻取樣的取樣間距
不超過臨界值1/2B
註： 只有帶限函式才能由它的取樣值確定。
故而通過取樣後即可得到時域離散信號。
說明：
① 其中 T 在取樣過程中是重要參數，但在結果中卻並不重要。
② 信號要進行計算機處理（數字處理） ，必須要離散化、數位化；
③ 數位訊號處理時，nT 並不重要（特別在非實時處理中） ，重要的是離散時間序列。
④ x(n) 中 n 是整數，表示取樣編號，所有取樣點的集合便是數字序列 x(n)。
基本離散時間序列
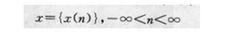圖4時域離散信號可以用一個離散時間的數字序列來表示。
其中n為整數。因此，它們是離散時間變數n的函式。信號x(n)是序列x中的第n個值。
常用的時域離散信號有單位抽樣序列、單位階躍序列、指數序列及正弦序列。
時域離散信號系統
時域離散信號系統是輸入與輸出均為時域離散信號的系統，本質上即處理時域離散信號的系統，它的功能是對輸入信號序列進行變換後再輸出。時域離散信號系統的數學定義是把輸入信號序列x(n)通過一個運算元映射為輸出信號序列：y(n)。定義y(n)=T[x(n)]，其中，y(n)為輸出信號序列，T為變換運算元，而x(n)為輸入信號序列。在數位訊號處理中廣泛套用的數字濾波器 就是一種典型的時域離散信號系統。它的功能是把輸入的時域離散信號序列按照預定的要求轉換成輸出信號序列，即保持輸入信號中的必要成分，濾除其中的多餘或噪聲成分。用近代數位訊號處理方法來對信號進行處理的系統，均屬於時域離散信號系統，包括快速傅立葉變換，頻域或時域的增強處理，分析與合成，以及自適應濾波等。時域離散信號系統已經廣泛地套用於電信及其它實用部門。例如回波抑制器，如果完全採用新型數位訊號處理器或其他數字元件來實現時，它就是一個時域離散信號系統。
離散時間信號的基本運算
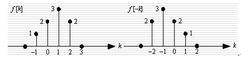圖5 翻轉1. 翻轉
將 f [k] 以縱軸為中心作180度翻轉
2. 位移
3. 尺度變換
在原序列中每隔M-1點抽取一點
時域離散信號4. 序列相加
指將若干離散序列序號相同的數值相加
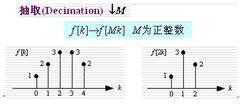圖7 尺度變換
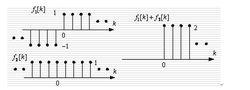圖8 序列相加5. 序列相乘
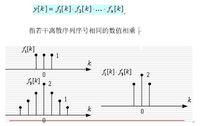圖9 序列相乘6. 差分
7. 求和
圖10 差分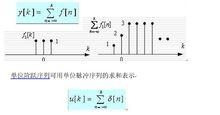
圖11 求和離散時間序列的表示
1 ．序列的單位脈衝表示法
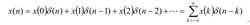圖12任何序列都可用移位和尺度後的單位脈衝序列加權和求得：
其中，x(0)、x(1)、x(2) ….. 代表信號取樣值。
由於δ(n-k) 在 k=n 時為 1，k≠n 時δ(n-k)=0，上式中無窮級數中只有一項非 0，即
n=k。因此，對於某一個 n 值，x(n) 等於這一點的取樣值 x(k)。
2 ．奇對稱和偶對稱
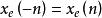時域離散信號一個實數序列 x e (n) 被稱為偶對稱，如果
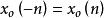時域離散信號同樣，一個實數序列 x o (n) 被稱為奇對稱，如果
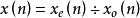時域離散信號這樣任何任意實數序列 x(n) 可分解成偶對稱和奇對稱兩部分：
