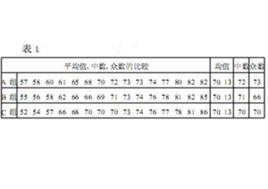
算數平均數
算術平均數是全部數據的算術平均,又稱均值,符號為M(Mean)。算術平均數是集中趨勢作主要的測度值,在統計學中具有重要地位, 是進行統計分析和統計推斷的基礎。它主要適用於數值型數據,但不適用品質數據。根據表現形式的不同,算術平均數有不同的計算形式和計算公式。其中,算術平均數是加權平均數的一種特殊形式(它特殊在各項全相等),在實際問題中,當各項權不相等時,計算平均數時就要採用加權平均數,當各項權相等時,計算平均數就要採用算數平均數。兩者不可混淆。
簡單算術平均數
簡單算術平均數主要用於未分組的原始數據。設一組數據為X1,X2,...,Xn,簡單的算術平均數的計算公式為:
M=(X1+X2+...+Xn)/n
例如,某銷售小組有5名銷售員,元旦一天的銷售額分別為520元、600元、480元、750元和500元,求該日平均銷售額。
平均銷售額=(520+600+480+750+500)/5=570(元)
計算結果表明,元旦一天5名銷售員的平均營業額為570元。
拓展:一組數據X1,x2...Xn在數a上下波動,則,原數據分別減掉a,得到一組新數據
X1'=X1-a X2'=X2-a .......Xn'=Xn-a
所以X1=X1'+a X2=X2'+a........Xn=Xn'+a
所以:平均數=(X1+X2+....+Xn)/n
將上面的 X1'=X1-a X2'=X2-a .......Xn'=Xn-a 代入
得到了:(X1'+X2'+....+Xn')/n+a
即=x'拔+a
所以:x拔=x'拔+a
優缺點
算數平均數具備了良好集中量數應具備的一些條件:
1、集中量數
2、反應靈敏
3、確定嚴密
4、簡明易解
5、計算簡單
6、適合進一步演算
7、較小受抽樣變化的影響等優點。
同時也存在一定的缺點,限制了它的使用:
1、算術平均數易受極端數據的影響,這是因為平均數反應靈敏,每個數據的或大或小的變化都會影響到最終結果。
2、若出現模糊不清的數據時,無法計算平均數。
套用原則
1、同質性數據
2、平均數與個體數值相結合考慮
3、平均數於方差、標準差相結合考慮
中數
概念
中數(Median),又名中位數。 對一組數進行排序後,正中間的一個數(數字個數為奇數);或者中間兩個數的平均數(數字個數為偶數)。
中數是按順序排列在一起的一組數據中居於中間位置的數,即在這組數據中,有一半的數據比它大,有一半的數據比它小。這個數可能是數據中的某一個,也可能根本不是原有的數。
優點
1、計算簡單
2、容易理解
3、不受極端值影響
缺點
1、反應不夠靈敏
2、 受抽樣影響較大
3、中數乘以總次數於總數不相等
4、不能進一步代數運算
套用情況
1、需要快速估算集中值時
2、有極端數據時
3、有模糊不清楚的數據時
眾數
概念
眾數(Mode),一組數據中出現次數最多的數值,叫眾數,用M表示。
計算方法
(一)、根據單項數列求眾數,不需要任何計算,可以直接從分配數列中找出出現次數或頻率最大的一組標誌值,就是所求的眾數。
(二)、對組距數列求眾數。對眾數的計算有兩種公式:
1、上限公式:
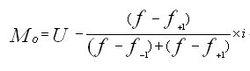 集中量數
集中量數2、下限公式
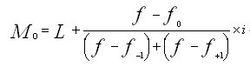 集中量數
集中量數其中:
f表示眾數所在組次數;
f-1表示眾數所在組前一組的次數;
f+1表示眾數所在組後一組的次數;
L表示眾數所在組組距的下限;
U表示眾數所在組組距的上限;
i表示組距;
優點
1、簡單明了
2、容易理解
缺點
1、不穩定,受分組和樣本變動影響
2、反應不靈敏
3、不能進一步做代數運算
套用
1、需要快速估算一組數據集中值時。
2、數據不同質時
3、兩極端有極端值時
4、快速估計分布形體時
關係
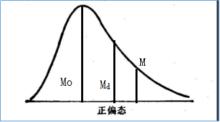 三者關係
三者關係在一個 常態分配中,平均數、中數、眾數三者相等,因此在數軸上三個
集中量數完全重合,在描述這種次數分布時,只需報告平均數即可。
在 正偏態分布中M>M>M
在 負偏態分布中M<M<M
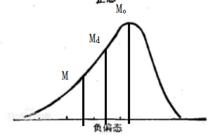 三者關係
三者關係M即平均數,M即中數,M即眾數