簡介
頻數 ：數據出現的頻率不同，我們稱每個對象出現的次數為頻數。
頻率 ：每個對象出現的次數與總次數的比值稱為頻率。
分布數列的種類：根據分組標誌的不同分為屬性分布數列和變數分布數列；變數分布數列又有單項式數列和組距式數列。任何一個分布都必須滿足：
1、各組的頻率大於0；
2、各組的頻率和等於1（或者說100%）
對於有序分類變數，除了給出各類別的頻數和頻率外，還有一個很重要的一方面：低於或者高於某類別的取值的案例的頻數和頻率。因為，個案之間是有等級的，知道比它們高的或者比它們低的頻數或者頻率，是有用的。但是，特別注意的是，統計軟體只能按照類別編碼從小到大進行頻數和百分比的累計，如果編碼不符合要求，就需要手工統計。所以，正確的編碼至關重要。
步驟
按照某種標誌（性質或數量）將數據分成若干組，分別統計各組數據的頻數（有時包括頻率）， 以反映數據分布在各組的情況。分組標誌以及與各組對應的頻數（或頻率） 是頻數分布的主要部分。當分組標誌是數值大小時，作頻數分布的步驟是：（1）求全距；（2）決定組距和組數；（3）列出組限；（4）統計各組頻數或頻率。頻數分布可用表格或圖形來表示，分別叫作頻數分布表或頻數分布圖，便於直觀地反映數據的一些分布規律。
類型
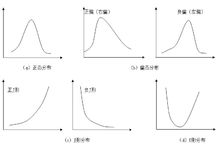
在日常生活和經濟管理中，常見的頻數分布曲線主要有鐘形分布（常態分配、偏態分布）、J形分布、U形分布，洛倫茨分布曲線等幾種類型。
鐘形分布特徵是“兩頭小，中間大”，即靠近中間的變數值分布的次數多，靠近兩邊的變數值分布的次數少。
J形分布主要有正J形和反J形分布。正J形是次數隨著變數值的增大而增多，反J形是次數隨著變數值增大而減少。
U形分布的特徵與鐘形分布相反，靠近中間的變數值分布次數少， 靠近兩端的變數值分布的次數多。例如人口死亡現象按年齡分布便是如此。
洛倫茨分布曲線是美國統計學家格倫茨（M.Krenz）提出來的，專門用以檢定社會收入分配的平等程度。洛倫茨分布曲線運作有兩個條件：一是居民或家庭按收入水平分組，計算各級居民或家庭的比重；二是計算各組收入的比重。
1.鐘形分布特徵是“兩頭小，中間大”，即靠近中間的變數值分布的次數多，靠近兩邊的變數值分布的次數少。
2.J形分布主要有正J形和反J形分布。正J形是次數隨著變數值的增大而增多，反J形是次數隨著變數值增大而減少。
3.U形分布的特徵與鐘形分布相反，靠近中間的變數值分布次數少， 靠近兩端的變數值分布的次數多。例如人口死亡現象按年齡分布便是如此。
4.洛倫茨分布曲線是美國統計學家格倫茨（M.Krenz）提出來的，專門用以檢定社會收入分配的平等程度。洛倫茨分布曲線運作有兩個條件：一是居民或家庭按收入水平分組，計算各級居民或家庭的比重；二是計算各組收入的比重。
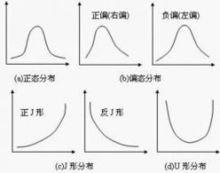圖1幾種常見的頻數分布