階躍函式符號及定義式
單位階躍函式
單位階躍函式用ε(t)表示,其定義式如下:
t<0時,ε(t)=0;
t>0時,ε(t)=1;
該定義式表明,在該函式t<0時,其值為0,;t>0時,其值為1;當t=0時,發生跳變,其值未定,而當t由負值或正值趨近於0時,其值則是確定的,即ε(t=0-)=0,ε(t=0+)=1。
階躍函式可以用來描述開關動作。
移位的單位階躍函式
單位階躍函式用ε(t-t0)表示,其定義式如下:
t<t0時,ε(t)=0;
t>t0時,ε(t)=1;
該定義式表明,在該函式t<t0時,其值為0,;t>t0時,其值為1;當t=0時,發生跳變,其值未定。
單位衝激函式與單位階躍函式之間的關係
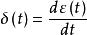 階躍回響
階躍回響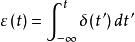 階躍回響
階躍回響即單位衝激函式等於單位階躍函式對時間變數的導數。反之,單位階躍函式等於單位衝激函式的積分。
階躍回響的定義
階躍回響g(t)定義為:系統在單位階躍信號u(t)的激勵下產生的零狀態回響。
在電子工程和控制理論中,階躍回響是在非常短的時間之內,一般系統的輸出在輸入量從0跳變為1時的體現。
階躍回響的圖像
在回響初期會產生一定的波動,之後便會向穩定值逼近,直至可以判定為穩定狀態。
 階躍回響
階躍回響數學模型
非線性系統
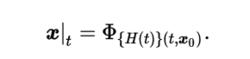 階躍回響
階躍回響當系統為非線性系統時,階躍回響被定義為:右圖的公式
為了強調這個概念所以將H(t)顯示為下標。
線性系統
對於線性時不變網路,階躍回響可以通過Heaviside階躍函式和系統本身的脈衝回響h(t)的卷積求得
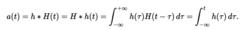 階躍回響
階躍回響其對於LTI系統的效果等效於僅僅集成後者。 相反,對於LTI系統,階躍回響的導數產生脈衝回響:
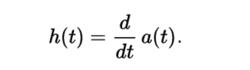 階躍回響
階躍回響然而,這些簡單的關係對於非線性或時變系統是不成立的。
實際意義
從實際的角度來看,了解系統如何回響是非常重要的,因為與長期穩定狀態大的與快的偏差可能對組件本身和取決於該組件的整個系統的其他部分產生具有劇烈的影響。此外,整個系統不能回響,直到組件的輸出穩定到其最終狀態的某個附近,從而延遲了整個系統回響。因此,了解系統的階躍回響給出關於這種系統的穩定性以及當從另一個系統啟動時達到一個靜止狀態的能力的信息。

