積分不等式

積分不等式是分析數學中常用到下列積分不等式。

積分不等式

正文

分析數學中常用到下列積分不等式。
楊不等式　設ƒ(x)是定義在【0, A】上滿足ƒ(0)=0的嚴格單調增加的連續函式,ƒ-1(y)是ƒ(x)的反函式,則對任何

α∈【0,A】，b∈【0,ƒ(A)】，

有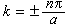

若且唯若ƒ(α)=b時，上式中等號成立(見圖)。
特別，當ƒ(x)=xα(α>0)時，令

由楊不等式得到

若且唯若b=αp-1時，上式中等號成立。
赫爾德不等式 設(X,φ,μ)是測度空間(見測度論)，E ∈φ，ƒ(x)、g(x)分別在 E上p 次、q次可積，則 ƒ(x)g(x)在E上可積,並且

上式中等號成立若且唯若存在實數θ以及不全為零的實數с1和с2，使得等式

argƒ(x)g(x)=θ , с1|ƒ(x)|p=с2|g(x)|q

在E上幾乎處處成立。
由積分的赫爾德不等式立即可得級數的赫爾德不等式：設

式中p>1，q>1 ，則絕對收斂，並且

。

上式中等號成立若且唯若存在實數θ 以及不全為零的非負實數 с1 和 с2，使對一切自然數 n，argαnbn=θ，且
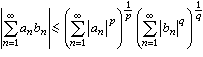施瓦茲不等式　赫爾德不等式中用得最普遍的是p=q=2的情況，此時的赫爾德不等式稱為施瓦茲不等式,有時也稱為柯西不等式或布尼亞科夫斯基不等式。它的積分形式、級數形式分別為

上面兩式中等號成立的充要條件分別是存在兩個不全為零的常數с1和с2，使得

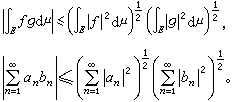
с1ƒ(x)=с2g(x)

在E上幾乎處處成立和對一切自然數n，с1αn=с2bn。
閔科夫斯基不等式　設(X,φ,μ是測度空間，E∈φ，ƒ(x)，g(x)都是E上p次(p≥1)可積函式，則ƒ(x)+g(x)在E上p次可積，並且

。

當p>1時,上式中等號成立的充要條件是存在不全為零的非負實數с1和с2，使得

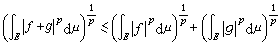с1ƒ(x)=с2g(x)

在E上幾乎處處成立；當p=1時，上式中等號成立的充要條件是，argƒ(x)=argg(x)在E上幾乎處處成立。
由積分的閔科夫斯基不等式，可得級數的閔科夫斯基不等式：如果，p≥1，則

當p>1時,上式中等號成立若且唯若存在不全為零的非負實數с1和с2,使對一切自然數n,с1αn=с2bn；當p=1時,上式中等號成立若且唯若對一切自然數n，argαn=argbn。
延森不等式　設φ(x)是【α,b】上有限實函式,如果對任何x1,x2∈【α,b】以及任何正數p1、p2，都有

則稱φ為【α,b】上的下凸函式。如果φ(x)是【α,b】上的下凸函式，則對任何x1,x2,…,xn∈【α,b】以及任何正數p1,p2,…,pn，有延森不等式：

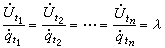積分形式的延森不等式:設φ(x)是【α,b】上的下凸函式，又設(X,φ,μ)是測度空間，E∈φ,p(x)是E上非負可積函式，並且,而ƒ(x)是E上可測函式，並且α≤ƒ(x)≤b，則

。

配圖

相關連線