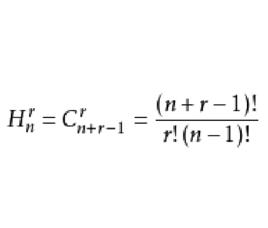基本介紹
定義
 重複組合
重複組合 重複組合
重複組合 重複組合
重複組合 重複組合
重複組合 重複組合
重複組合一般地,從個不同的元素中,每次取出個可以重複的元素並成一組,叫做從個不同的元素每次取出個元素的允許重複的組合,即 重複組合,其組合總數記作。
相關結論
關於重複組合的計數方法有下面的規律。
 重複組合
重複組合 重複組合
重複組合定理1 從個不同的元素每次取出個元素的允許重複的組合總數為
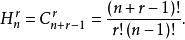 重複組合
重複組合 重複組合
重複組合 重複組合
重複組合證法1:設有個不同的元素,不失一般性,可設為。
 重複組合
重複組合 重複組合
重複組合設從這個不同的元素取出個元素的重複組合為
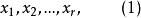 重複組合
重複組合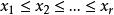 重複組合
重複組合且假定,這裡有等號出現是因為元素允許重複。
我們再構造一個組合
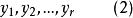 重複組合
重複組合與組合(1)相對應,其對應關係是
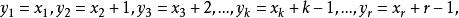 重複組合
重複組合顯然這種對應是一一對應。
在這個對應中,雖然組合(1)中的元素有可能相同,但是組合(2)中的元素卻都不相同,這樣,組合(2)就是一個沒有重複元素的組合。
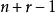 重複組合
重複組合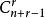 重複組合
重複組合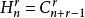 重複組合
重複組合組合(2)是從個不同的元素中,取出r個不同元素的組合,組合數為。由於組合(2)的組合數與組合(1)的組合數相同,所以組合(1)的組合數為。
關於這個證明,我們給出一個直觀的例子:
 重複組合
重複組合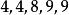 重複組合
重複組合例如,從中取出5個允許重複的組合,其中一個組合是。
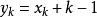 重複組合
重複組合對於這個組合,採用證法中的構造方法,就是
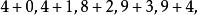 重複組合
重複組合即
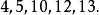 重複組合
重複組合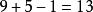 重複組合
重複組合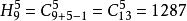 重複組合
重複組合這第二個組合的元素沒有重複,第二個組合相當於從(個)元素中取出5個不同元素的組合。組合數為。
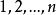 重複組合
重複組合證法2: 設有n個不同的元素,不失一般性,可設為。
 重複組合
重複組合從個不同的元素取出r個元素的重複組合為
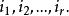 重複組合
重複組合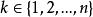 重複組合
重複組合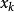 重複組合
重複組合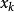 重複組合
重複組合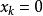 重複組合
重複組合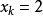 重複組合
重複組合設元素在組合中出現了次,其中是非負整數,若,則說明元素k在組合中沒有出現;若,則說明元素k在組合中出現2次;……
由此,一次不定方程
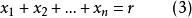 重複組合
重複組合 重複組合
重複組合的任一組非負整數解就對應著一個個元素的重複組合。
 重複組合
重複組合 重複組合
重複組合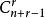 重複組合
重複組合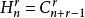 重複組合
重複組合所以,從個不同的元素取出個元素的重複組合數,就是一次不定方程③的非負整數解的個數,其個數為,即。
我們也給出一個例子來說明這個證法。
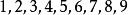 重複組合
重複組合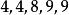 重複組合
重複組合例如,從中取出5個允許重複的組合,其中一個組合是,對應著一次不定方程
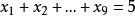 重複組合
重複組合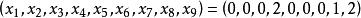 重複組合
重複組合的一組解。
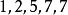 重複組合
重複組合同樣,組合對應著解
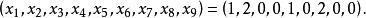 重複組合
重複組合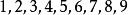 重複組合
重複組合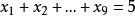 重複組合
重複組合所以,求從中取出5個允許重複的組合數的問題就轉化為一次不定方程的非負整數解問題,即
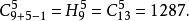 重複組合
重複組合例題解析
例1 郵局發行10種新郵票,有一個集郵愛好者購買了15張郵票,他有多少種買法?
解: 買郵票的任何一種方式都可以看做是從10個元素中取出15個元素的組合,因此買法種數為
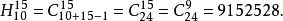 重複組合
重複組合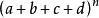 重複組合
重複組合例2 求的展開式的項數。
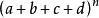 重複組合
重複組合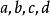 重複組合
重複組合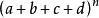 重複組合
重複組合解:由於的展開式的每一項都是n次的,因此,展開式的每一項都是從這4個元素中取出n個元素的重複組合,不同的組合就得到不同的項,所以,的展開式的項數為
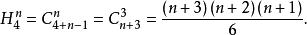 重複組合
重複組合例3 有一枚硬幣,正面是國徽,反面是幣值,我們同時投擲5枚這樣的硬幣,會出現多少種不同的情況呢?
把各種不同的情況一一列舉出來就是:
| 正面 | 5 | 4 | 3 | 2 | 1 | 0 |
| 反面 | 0 | 1 | 2 | 3 | 4 | 5 |
如果我們把硬幣的“正面”和“反面”看成兩個不同的元素,那么這個問題就是:從兩個不同的元素中,取出5個元素的組合,顯然,所取的元素允許重複。
 重複組合
重複組合又如,從3個元素的集合中,取2個元素,如果允許所取得元素重複,則有
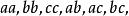 重複組合
重複組合共6種 。