概念
重整化群是一個在不同長度標度下考察物理系統變化的數學工具。標度上的變化稱為“標度變換”。重整化群與“標度不變性”和“共形不變性”的關係較為緊密。共形不變性包含了標度變換,它們都與自相似有關。在重整化理論中,系統在某一個標度上自相似於一個更小的標度,但描述它們組成的參量值不相同。系統的組成可以是原子,基本粒子,自旋等。系統的變數是以系統組成之間的相互作用來描述。
基本原理
 重整化群
重整化群 重整化群
重整化群 重整化群
重整化群以量子電動力學為例。利用Feynman展開的微擾論方法,我們計算一個物理量,比如電子之間的散射率,會得到一個按照耦合常數 展開的級數,每一項的係數是粒子動量 的積分式。這樣的積分式會出現紫外發散,即 允許的取值可以到無窮大時,係數趨向於正或負無窮,這使得整個理論失去意義。
 重整化群
重整化群 重整化群
重整化群 重整化群
重整化群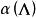 重整化群
重整化群 重整化群
重整化群 重整化群
重整化群 重整化群
重整化群 重整化群
重整化群 重整化群
重整化群 重整化群
重整化群 重整化群
重整化群 重整化群
重整化群 重整化群
重整化群 重整化群
重整化群 重整化群
重整化群 重整化群
重整化群 重整化群
重整化群 重整化群
重整化群 重整化群
重整化群 重整化群
重整化群 重整化群
重整化群為了克服這一困難,人們引入了重整化方法。用這個方法,我們首先對所有的積分作紫外截斷,從而得到有限結果。顯然,這樣得到的展開係數將與截斷有關。但是,在連續場論中這個截斷是人為引入的,物理上並不存在。為了解決這個問題,對於任意,我們要求可以重新定義一個相應的耦合常數,使得計算最後給出的物理量與無關。在量子電動力學和其他可重整的理論中,這是可以做到的。換句話說,對於微擾展開的任意級次,可以定義該系統的一系列和截斷相關的參數,使得系統在動量遠小於時的物理性質和無關。由於實際的最後要取為無窮大,也就是說,系統在任意有限動量上的物理性質和無關,於是,我們要求理論具有這樣的不變性:當改變一個比例時,耦合常數將作相應的變化,而最後給出的結果將是與無關的。這也就導致了重整化群的想法。也就是說,對於改變一個比例這種變換的全體有一個類似群的結構,即滿足組合律;先改變比例為,再接著改變比例為得到的耦合常數等於作一次改變比例為得到的耦合常數。但嚴格說起來,這並不是一個群,而是一個所謂的半群。原因是在上述定義下,我們無法定義逆變換。
 重整化群
重整化群現在,我們把寫成
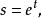 重整化群
重整化群並令
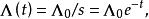 重整化群
重整化群 重整化群
重整化群 重整化群
重整化群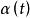 重整化群
重整化群 重整化群
重整化群其中是一個固定的數。如上所述,為使得最後結果有物理意義,我們要讓耦合常數也作相應的改變,即也隨參量改變。並令
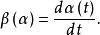 重整化群
重整化群 重整化群
重整化群由此,我們可以定義所謂函式。它是重整化群理論中最重要的一個物理量,決定了相應的相互作用在整個理論框架下所起的作用。

