基本內容
磁場力包括磁場對運動電荷作用的洛侖茲力和磁場對電流作用的安培力,安培力是洛侖茲力的巨觀表現.磁場力現象中涉及3個物理量的方向:磁場方向、電荷運動方向、洛侖茲力方向;或磁場方向、電流方向、安培力方向.我們用左手定則說明3個物理量的方向時有一個前提,認為磁場方向垂直於電荷運動方向或磁場方向垂直於電流方向.不少同學認為,根據左手定則知道其中任意2個量的方向可求出第3個量的方向.一般說,這種看法是不正確的.
事實是,磁場方向不一定垂直於電荷運動方向或電流方向,它們之間的夾角可以是任意的.我們能肯定的是:洛侖茲力一定既垂直於磁場方向又垂直於電荷運動方向,洛侖茲力垂直於磁場B和電荷運動速度v所決定的平面.安培力一定既垂直於磁場方向又垂直於電流方向,安培力垂直於B和I所決定的平面,我們不應該忽視一個重要事實:B與v或I平行時,洛侖茲力或安培力都不存在.
因此,當B⊥v或B⊥I時,我們可以用左手定則表述3個物理量方向間的關係.這時,知道任意2個物理量的方向可求出第3個物理量的方向.當B與v或B與I不垂直時,根據B與v的方向或B與I的方向,可確定洛侖茲力f或安培力F的方向,但是,根據v、f的方向或I、F的方向不能唯一的確定B的方向;根據B、f的方向或B、F的方向不能唯一確定v或I的方向.這2種問題若有唯一確定的解必須補充條件.
例1 如下圖所示,電流I指向Z軸正向,I所受安培力F指向Y軸正向,則磁感應強度B的方向().
A.一定指向X軸正向
B.一定指向X軸負向
C.在XOY平面內,與Y軸夾角大於π/2小於π
D.無法判定
分析和解 根據左手定則可判定出B的一個分量的方向沿X軸正向.B的另一個分量沿Z軸正向或負向.所以,B的方向在XOZ平面內,B與Z軸的夾角在O到π之間,認為B的方向一定指向X軸正向是錯誤的,認為B一定指向X軸負向或認為B在XOY平面內更是錯誤的.本題B的方向無法確切判定,正確的是D.
例2 一個帶正電的粒子以速度v1,在XOY平面內運動時,它所受勻強磁場B的洛侖茲力f1的方向指向Z軸負方向,如果此粒子以速度v2沿Z軸正向運動,則粒子所受洛侖茲力f2的方向指向X軸正向,由此可知B的方向( ).
A.一定指向X軸正向
B.一定指向Z軸正向
C.一定指向Y軸負向
D.一定指向X軸負向
分析和解 根據題意畫出示意圖如上圖所示,由洛侖茲力f1的方向知B的方向在XOY平面內,由洛侖茲力f2的方向知B的方向在YOZ平面內,XOY平面與YOZ平面的交線就是Y軸的直線,根據v2和f2的方向,用左手定則判定出B的方向指向Y軸負向,C正確.
例3 一束速度相同的電子通過勻強磁場B和勻強電場E同時存在的區域而沒有發生偏轉,則以下對此區域內B、E方向的判斷中正確的是( ).
A.B一定垂直於E
B.B一定平行於E
C.B與E的夾角不能確定
D.B與E可能垂直也可能平行
分析和解 電子束通過B、E同時存在的區域而沒有發生偏轉有2種情況:電子勻速通過這區域,電子所受電場力與洛侖茲力平衡;電子作勻變速直線運動通過這區域,電子只受電場力作用.
當電子只受電場力不受洛侖茲力作用時,電子做勻加速或勻減速直線運動,這時電場強度E的方向與電子運動方向平行,磁感應強度B的方向也與電子運動方向平行,也就是B與E的方向平行.
當電子所受電場力與洛侖茲力平衡時,電子做勻速直線運動通過這區域,電子所受洛侖茲為fm的方向與電子速度v垂直,電子所受電場力fe的方向與fm的方向相反.所以,電場E的方向與v垂直.而由v、fm的方向可知,磁場B的一個分量的方向與v垂直,也與E垂直,B的另一個分量的方向與v平行.所以,B與v的夾角不能確定,B與E的夾角也不能確定.C、D正確.
例1和例3中只知道安培力、洛侖茲力方向,不能唯一確定磁場B的方向,這是因為我們不能排除B可能有一個與電流I或粒子速度v平行的分量.例2中知道粒子速度為v1時f1的方向,又知道粒子速度為v2時f2的方向,也即補充了條件,因此才能唯一確定B的方向.
例4 如下圖所示,質量為m、長為l的一段導線放在傾角為θ的光滑導軌上,導線中通入電流I,要讓導線靜止於導軌上,至少應加多大的勻強磁場B?
分析和解 導線受重力mg、導軌支持力N和磁場的安培力F作用,這3個力的合力為零導線才能保持靜止,由此可知3個力在同一豎直面內,如下左圖所示.我們還可以知道,F的方向在圖中兩虛線所圍的範圍內都能保持導線的平衡.
題目要求磁場B的最小值,所以F也要求是最小值.用力合成的三角形法則判定出F的方向應平行於導軌斜面向上,如上右圖所示,用左手定則判定出B的方向垂直斜面向下.
由上右圖知 mgsinθ=F=IlB,
垂直導軌面向下的勻強磁場才能使導線靜止在導軌上.
本題要求磁場的最小值,故磁場平行於導線電流方向的分量應為零,磁場方向一定垂直於導線,如果不是要求磁場的最小值,則磁場垂直於導線電流方向的分量有一分布範圍與安培力F的範圍相對應,由上面左圖中兩虛線所確定的F的範圍,用左手定則可確定B相應的範圍.
例5 空間中某一區域存在勻強磁場,為了確定磁場的方向、大小,我們做2個實驗.第1個實驗如下左圖所示,質量為m、帶正電q的粒子以速度v1向右運動時,粒子所受洛侖茲力f1的方向垂直紙面向里.第2個實驗如下右圖所示,當粒子以垂直紙面向外的速度v2運動時,粒子所受洛侖茲為f2的方向與v1方向的夾角為30°.試根據這2個實驗判定磁場的方向和大小.
分析和解 由第1個實驗中v1和f1的方向可知磁場B矢量一定在紙面內,B的一個分量垂直於v1向下,另一個分量平行於v1.即B矢量在v1所在直線的下方.
由第2個實驗中v2和f2的方向可知B矢量椂ㄔ謨隷f2垂直的平面內,這個平面與紙面相交的一條直線和v1的夾角為60°.所以,在第2個實驗中v2、B、f2兩兩互相垂直,我們用左手定則判定出B的方向如下圖所示.
根據洛侖茲力公式
B的大小的這2種表述應該是一致的.
本題說明,只根據運動粒子在磁場中做某一種運動時所受的洛侖茲力,不能確定磁場的方向.再做一次實驗或補充必要的條件才能確定磁場的方向.這是因為與粒子速度平行的磁場分量對粒子無作用力,不補充條件我們無法確定這一磁場分量,根據電流所受磁場的安培力來確定磁場的方向時,有類似的問題.
相關問題
與磁場力有關的兩類極值問題
磁場中的極值問題往往與磁場力有關,磁場中的極值問題按磁場力來分也可以分為兩類,一類是與安培力有關的極值問題,另一類是與洛倫茲力有關的極值問題。但不管求解哪一類極值問題首先要確定研究對象,搞好受力分析;然後根據受力情況和初始狀態,搞清研究對象的運動過程,再根據運動過程用相應的物理規律;最後是求得所需的物理量。
有安培力參與的極值問題
通電導線在磁場中不管是處於靜止狀態還是運動狀態,都可能會受到安培力的作用。但通電導線處於靜止狀態時,它本身不會產生電動勢,而處於運動狀態時,通電導線由於電磁感應它本身也會產生感應電動勢,因此在求解運動狀態的通電導線的極值問題時,不能忘掉這個感應電動勢。
1.1 通電導線靜止時的極值問題
例1 如圖1所示銅棒質量為0.1kg,靜止於相距8cm的水平軌道上,兩者間的動摩擦因數為0.5。現從一軌道載送5A電流至另一軌道,欲使銅棒滑動,兩導軌間所加的勻強磁場的磁感應強度的最小值為多少䲁
 圖片1
圖片1解析 設安培力F與水平方向的夾角為θ,畫出如圖2所示的受力分析圖。則:
F = BIL。(1)
且銅棒在重力、支持力、安培力、摩擦力共同作用下應滿足:
Fcosθ-μ(mg-Fsinθ) =0。(2)
聯立(1)、(2)解得:
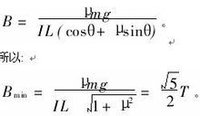 圖片2
圖片21.2 通電導線運動時的極值問題
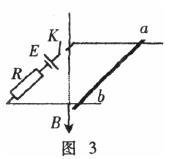
例2 如圖3所示,水平放置的兩平行金屬導軌之間的距離為L =0.25cm,電池的電動勢E=6V,內電阻r =0,電阻R =5Ω,勻強磁場磁感應強度B豎直向下,K合上後,橫放在導軌上的金屬棒ab在磁場力作用下由靜止開始向右運動,金屬棒與導軌間的滑動摩擦力f=0.15N,為使棒運動速度最大,B應為多大䲁此時Vmax等於多少䲁
 圖片4
圖片4解析 金屬棒運動時會產生感應電動勢,此電動勢方向與電池電動勢方向想反,則電路中的電流大小為:I = (E-BLv)/R。(1)當金屬棒速度最大時,加速度應為零,則:BIL-f =0。(2)把(1)代入(2)得:
有洛倫茲力參與的極值問題
2.1 只有洛倫茲力作用時的極值問題 當題中只有一個帶電粒子的運動時,往往只需一條運動軌道就可確定粒子的極值問題,而當涉及到多個帶電粒子的運動時往往需要多條軌道才能確定帶電粒子的極值問題。
 圖片5
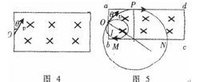
圖片5例3 如圖4所示,一足夠長的矩形區域abcd,存在磁感應強度為B垂直紙面向里的勻強磁場。在ab的中點O處,垂直磁場射入一速度方向跟ab邊夾角為30°,速度大小為v的帶電粒子,已知粒子的質量為m、電量為e,ab邊的長度為 ab邊足夠長,粒子重力忽略不計。問:電子全部從bc邊射出時,電子入射速度v大小的數值範圍如何䲁解析 從帶電粒子在磁場中做勻速圓周動的半徑公式可知,半徑越小,帶電粒子的運動速度越小;半徑越大,帶電粒子的運動速率越大。因過圓周上某點的軌道半徑總與該點的速度方向垂直,可知最大軌道半徑和最小軌道半徑的圓的圓心都在初速度方向的垂線上。由此可畫出如
圖5所示的示意圖。當軌道半徑最小時電子從bc邊上的M射出,當軌道半徑最大時,電子剛好不從ad邊射出。設最大速率、最小速率分別為v1、v2,最大半徑分別為R1、R2,則由圖中的幾何關係可得:
R1(1-sinθ) =1/2。(1)
R2(1+sinθ) =1/2。(2)
因θ=30°,代入上面兩式可得:
R1=1,R2=1/3。(3)
又從洛倫茲力作為向心力可得:
Bev = mv2/R。(4)
由以上四式可得粒子從bc邊上射出v的數
值大小範圍為:
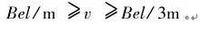 圖片6
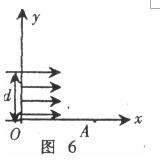
圖片6例4 如圖6所示,在平面直角坐標系的第一象限內,有一束寬為d的電子流,其中每個電子的速度均為v,都平行於Ox軸向右勻速運動,已知電子的質量為m、電量為e,圖中A點的坐標為(1,0),且1> d,現要求這束電子通過垂直於xOy平面的勻強磁場之後都能通過A點,且距離x軸為d的電子經磁場偏轉後恰好垂直x軸通過A點。求:(1)這個區域內磁場的磁感應強度B的大小和方向。(2)設計一個符合上述條件且面積最小的勻強磁場區域,求出它的面積,並在xOy平面上畫出磁場邊界。
 圖片7
圖片7解析
(1) 如圖7所示,先考慮與x軸距離為d的電子,它經磁場偏轉後恰好垂直通過x軸上的A點,由左手定則可知磁場方向垂直紙面向里,電子的軌道半徑R = d。(1)又有電子受的洛倫茲力作為向心力得:Bev = mv ^2/R。(2)聯立(1)、(2)兩式解得:B = mv/ed。
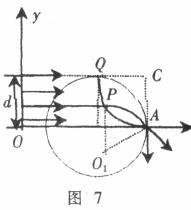
(2) 從圖7中可以看出與x軸距離為d的電子通過磁場偏轉後恰好垂直通過A,圓弧QA應是所求磁場區域的上邊界。為確定下邊界,我們考察與x軸距離為y的電子的運動,設它從P(x,y)點入射磁場,通過磁場偏轉後通過A點,則電子在磁場中的運動軌道是以O1為圓心、d為半徑的一段圓
 圖片8
圖片8 圖片9
圖片92.2洛倫茲力和其它外力共同作用下的極值問題
在此種情況下電荷的運動沒有象前一種那么簡單。在一些問題中它是在直線運動,而在另一些問題它是曲線運動,電荷做什麼運動要視具體情況而定。
例5 如圖8,質量為0.1g的小球帶電4×10-4C的電量,把它套在
很長的絕緣直棒上,將此棒豎直地放入相互平行且都是水平的勻強電場和勻強磁場中,起場強E=10N/C,磁感應強度B=0.5T,若小球與棒之間的動摩擦因數為0.2,求小球沿棒下滑的最大速度。
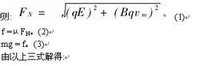 圖片10
圖片10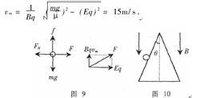 圖片12
圖片12解析 畫出如圖9所示的受力分析圖。小球受重力、電場力、洛倫茲力、彈力和摩擦力的作用,當合力為零時,小球下滑的速度達到最大。(圖9中F表示電場力和洛倫茲力的合力)例6 如圖10,頂角為2θ的光滑圓錐固定在勻強磁場中,一質量為m,電量為q的小球沿
錐面做勻速圓周運動,它的最小半徑是多少䲁
解析 如圖11,小球運動中受到三個力作用:重力mg,支持力FN,洛倫茲力F = qvB。
由以下兩式:
FNsinθ-mg =0,
和qvB-FNcosθ= mv/r。
得:mv-qBrv+rmgctgθ=0。
因v的取值範圍為實數,故:
(qBr)-4mgrctgθ≥0,
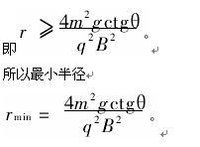 圖片13
圖片13
