定義
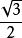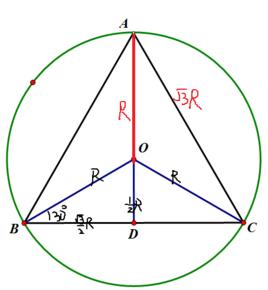
邊心距正六邊形的邊長就等於其外接圓的半徑,它的邊心距等於邊長的倍。正多邊形的邊心距就是其內切圓的半徑。正多邊形都有的外接圓，每條邊的中心角，實際上就是這條邊所對的弧的圓心角。
性質
如果用 a表示邊心距， s表示邊長， p表示多邊形的周長，正多邊形的面積可以分割成n個小三角形求和，最終結果表示為：
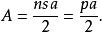邊心距其內切圓的面積可以表示為：
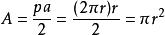邊心距做法和計算
已知正多邊形中心的情況下，邊心距可通過從正多邊形中心向某一邊作垂線段；或連線正多邊形中心和某一邊的中點求得。不知中心的情況下，可以根據垂徑定理，通過兩條邊的垂直平分線的交點來確定正多邊形的中心，然後求出邊心距。
邊心距可以通過正多邊形外接圓的半徑和邊長求出，如果正n邊形的外切圓的半徑為 R邊長為 s，則邊心距為:
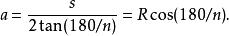邊心距正多邊形怎么求邊心距？
做其中兩邊的垂直平分線，得其交點是圓心。將各端點同圓心連起來，這就是半徑R。正N多邊形現在就有N條半徑，每兩條半徑之間的夾角就是360/N。邊長就是2Rsin(180/N)，邊心距就是Rcos(180/N)。周長就是2NRsin(180/N)，面積就是NRsin(180/N)Rcos(180/N)。
