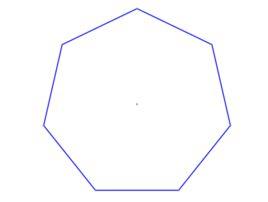
簡述
正七邊形不可以用尺規作圖畫出，但三角形、五邊形、十七邊形、二百五十七邊形卻可以作出（當然都是正的）。不過它卻可以用帶刻度的尺子和圓規作出。七邊形的內角和是900度，每個角是128.571428(571428循環）度.
正七邊形
七邊形
七邊形
七邊形正七邊形是指所有邊等長、所有角等角的七邊形，由七條相同長度的邊和七個相同大小的角構成，是一種正多邊形，因此在施萊夫利符號中可以用表示。正七邊形的內角是弧度，約為128.5714286度，其中角度的小數為循環小數，值為。
面積
正七邊形的面積（A）可以利用其邊長（a）來計算：
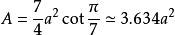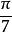七邊形。
七邊形將正七邊形的頂點與幾何中心相連可以將正七邊形分成七個扇三角形，這些三角形可再藉由邊心線將之一分為二。正七邊形的邊心距是正切值的一半，而這十四個小三角形的面積就會是四分之一倍的邊心距。
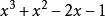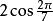七邊形
七邊形其確切的代數式是三次方程，其中的一個根為，在複數中表示為：
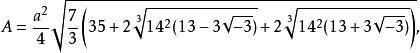七邊形其中，複數中的虛數部最後會互相抵銷使結果為實數。這個表達式不能被全部是實數的式子重寫，也不能透過化簡消去其虛數的部分。
對稱性
正七邊形的對稱群。頂點的顏色是依照其對稱特性繪製。
正七邊形具有14階的Dih二面體對稱，由於7是一個質數，因此其只有一個子群：Dih以及2個環形對稱群：Z和Z。
七邊三角形
若一正七邊形邊長為a、最短對角線為b、最長對角線為c，其滿足等式a<b<c
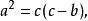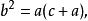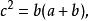七邊形
七邊形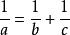
七邊形
七邊形（倒數和等式）
扭歪七邊形
扭歪七邊形，又稱不共面七邊形，是指頂點並非完全共面的七邊形。除了三維空間的扭歪七邊形之外，扭歪七邊形亦可以在一些高維度的多胞體中找到，通常會以皮特里多邊形的方式存在。例如六維正七胞體的皮特里多邊形就是一個扭歪七邊形，其具有A[3,3,3,3,3] 的考克斯特群的對稱性。
命名
七邊形的英文名稱是heptagon，而有時也叫做septagon，"sept-"（septua-的元音音節省略，是一個從拉丁語引進的數學前綴）來表示“七、七的”，而不是hepta-（一個從希臘語引進的數學前綴，套用於大多數英語中數學、化學等學術類術語命名的前綴）。
使用
於2006年，英國正流通兩種正七邊形硬幣，即大不列顛五十便士（50p）和大不列顛二十便士（20p）。二十歐分硬幣側表面上的凹形也使它與正七邊形極為相似。嚴格地說，這些硬幣的形狀是一個曲線的七邊形，它們被稱作定長曲線：這些外表面呈曲線的邊能夠便於硬幣在自動販賣機裡面更加流暢光滑地滾動。
在雙曲面上，正七邊形可構成正七邊形鑲嵌。
畫法
近似正七邊形的畫法如下：① 以定長R為半徑作圓，並過圓心O作互相垂直的縱橫兩條直徑MN、HP.② 過N點任作一射線NS，用圓規取七等分，把端點T與M連結起來，然後過NT上的各點推出MT的平行線，把MN七等分.③以 M為圓心，MN為半徑畫弧，和PH的延長線相交於K點，從K向MN上各分點中的偶數點或奇數點（圖中是 1、3、5、7各點）引射線，與交於A、B、C、M.再分別以 AB、BC、CM為邊長，在圓周上從A點（或M點）開始各截一次，得到其他三點，把這些點依次連結起來，即得近似的正七邊形。
自然界中
部分植物會以七邊形的方式生長，例如部分的仙人掌。
