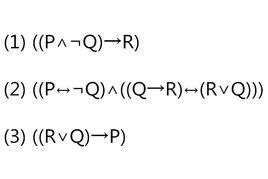基本介紹
命題公式是對由命題變項、聯結間和圓括弧按照一定邏輯關係構成的複合命題的形式化描述。。
定義 命題合式公式,又稱為 命題公式(簡稱公式),可按下列規則生成:
(1)命題變項是命題公式。
(2)如果A是命題公式,則¬A是命題公式。
(3)如果A和B是命題公式,那么(A∧B)、(A∨B)、(A→B)和(A↔B)都是命題公式。
(4)若且唯若有限次地套用(1),(2),(3)所得到的包含命題變項,聯結詞和圓括弧的符號串是命題公式。
命題公式的定義是一個遞歸定義形式。命題公式本身不是命題,沒有真值,只有對其命題變項進行賦值後,它才有真值。
5個聯結詞運算兒有不同的優先權。當它們同時出現在一個命題公式里時,聯結間運算的優先次序為¬、∧、∨、→、↔,如果有括弧,則括弧內的運算優先進行 。
例題解析
【例1】判定下列式子是否是命題公式。
(1) ((P∧¬Q)→R)
(2) ((P↔¬Q)∧((Q→R)↔(R∨Q)))
(3) ((R∨Q)→P)
(4) ((R,¬Q)→P)
(5) (R∧→Q)
(6) ((P∨Q)→(R↔¬Q))
解根據命題公式的定義可知1,(1)、(2)、(3)是命題公式,而(4)、(5)、(6)不是命題公式。命題公式最外層括弧可以省略。
有了命題公式的定義後,很多複合命題可以符號化為命題公式。
【例2】 “如果提高天然氣占能源的比例,且燒乾淨的煤,那么空氣品質就能提升許多。”用命題公式符號化該命題。
解:設P:提高天然氣古能源的比例; Q:燒乾淨的煤: R:空氣品質就能提升許多 。
該命題可符號化為(P∧Q)→R。
相關概念及定理
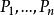 命題公式
命題公式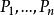 命題公式
命題公式定義1 設A是一個命題公式,是出現在A中的所有命題變項。對這些命題變項各賦予一個確定的真值,那這一組真值稱為對命題公式的一種賦值 。
對於不同的賦值,命題公式有不同的真值情況。將命題公式在所行的賦值下的真值情況用表格表達出來,這張表就稱為 真值表。如果一個命題公式有n個命題變項。每個命題變項有兩種真值情況,則共有2 種不同的賦值情況。為了不遺漏每種賦值情況。1個命題變項的取值一般從00...0到1...1或者從1...1到00...0。
 命題公式
命題公式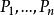 命題公式
命題公式 命題公式
命題公式定義2 設A、B是命題公式,是出現在A和B中的所有命題變項,如果對於的任何一組賦值,A的真值和B的真值都相同,則稱公式A等值於公式B(或A與B等值),記作AB。
因此,要判斷兩個公式是否等值,根據定義,只需將兩個公式的真值表列出,判斷兩個真值表是否相同即可。
對一個命題公式A,如果用公式B取代A中的一部分,會得到一個新公式C。但是一般來說,公式A和C是不等值的。例如,在公式P∧Q中用P∨¬P取代Q,得到的P∧(P∨¬P)不等值於原來的公式。但如果對取代過程加以某種限制,則得到的新公式會和原來的公式等值。
命題公式中有許多公式是等值的,要記住大量的等值公式是困難的,但一些基本的、重要的等值式模式是應該掌握的。下面列出一些最基本的等值式模式。
 命題公式
命題公式 命題公式
命題公式 命題公式
命題公式比如雙重否定律:¬¬AA,冪等律:A∨AA,A∧AA,還有交換律,結合律,分配律,德 摩根律,吸收律,同一律等。
定義3 設A是一個命題公式,A'是A的一部分,且A'也是一個命題公式,則稱A'是A的子公式。
 命題公式
命題公式 命題公式
命題公式定理 設A'是A的子公式,B'是一個命題公式且A'B'。將A中的A'用B'來取代,所得到的是一個新公式,記為B,則AB 。
命題公式的分類
重言式
給定一個命題公式,若對於其中的命題變項的任何一組賦值,命題公式對應的真值永遠為1,則稱該命題公式為重言式或永真式。
矛盾式
給定一個命題公式,若對於其中的命題變項的任何一組賦值,命題公式對應的真值永遠為0,則稱該命題公式為矛盾式或永假式。
可滿足式
給定一個命題公式,若至少存在一組賦值使得該公式的真值為1,則稱該命題公式為可滿足式。
由定義可知,公式¬(P∧Q)↔¬P∨¬Q是永真式,公式¬(P→Q)∧Q是永假式,永真式的真值總是為1,因而是一種特殊的可滿足式 。