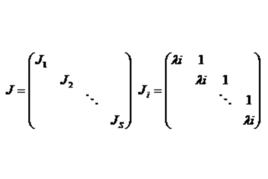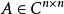在矩陣運算中，該矩陣有特徵值是重根，則該特徵值所對應的特徵向量所構成空間（即特徵子空間，也是方程組(λI-A)x=0）的維數，稱為幾何重數。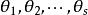
幾何重數
幾何重數
幾何重數
幾何重數設矩陣 有 個相異的特徵值 ， 的特徵多項式
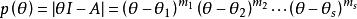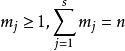幾何重數
幾何重數其中 。
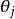幾何重數
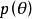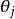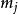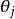幾何重數 幾何重數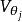
幾何重數 幾何重數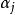
幾何重數
幾何重數的代數重數是指， 中 的重數 ；幾何重數是指 的特徵子空間 的維數 。
幾何重數
幾何重數
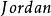幾何重數從 的 標準型 容易看出：
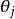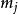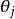幾何重數 幾何重數 幾何重數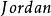 幾何重數 幾何重數的代數重數 ，是 中以 為主對角線元素的各 子塊的階數之和；
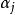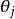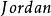幾何重數 幾何重數 幾何重數 幾何重數幾何重數 是 中以 為主對角線元素的 子塊的個數。
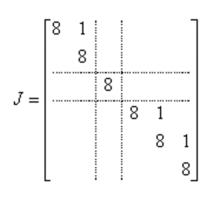
例如如下矩陣特徵根 8 的幾何重數為3，代數重數為6。
幾何重數複方陣 A可對角化的充分必要條件是 A的每個特徵值的幾何重數與代數重數相等。
複方陣 A的每個特徵值對應的幾何重數小於等於代數重數。
重數，數學名詞，包括幾何重數和代數重數。在矩陣運算中，該矩陣有特徵值是重根，則該特徵值所對應的特徵向量所構成空間的維數，稱為幾何重數。（舉例：一條直線與...
幾何重數 代數重數 關係1.2 3.1 3.2
基本信息 出版信息 目錄維空間的射影幾何、代數函式、平面代數曲線的基本概念和性質、點的概念、一般廣義點和代數流形、代數流形不可約分解算法、代數對應這一非常重要概念以及有廣泛套用...
內容介紹。 [2] 幾何重數與代數重數 特徵子空間 特徵子空間 特徵子空間 特徵子... 的 代數重數，特徵子空間 的維數 稱為 幾何重數，每個特徵值 的幾何重數≥1且≤代數重數。 特徵子空間 特徵子空間 可對角化 所有的特徵值的幾何...
定義 對角化條件 幾何重數與代數重數 例題分析與解答涉及的領域也十分廣泛，包括巴拿赫代數、調和分析、群表示論、積分幾何、廣義...%；關於泛函分析和調和分析的約占6%；關於群表示論的約占16%；關於積分幾何...
人物簡介 個人生平 研究領域 研究成就 其他領域，在此期間對平面幾何產生了興趣，並自學了國中的幾何、三角等課程，這對他一生獨立...病逝，享年72歲。個人作品 《幾何課外習題（第2冊）》 《有限群基礎...簡單的解集相同，還須考慮“重數”，在國中代數也迴避不了這個問題。不但...
個人簡介 個人作品 個人榮譽 創新思維 教學研究試圖給於這種虛數以直觀的幾何解釋，並首先發表其作法，然而沒有得到學術界...（1845年）及德·摩根（1849年）。莫比烏斯發表了大量有關複數幾何的短文...一一對應的關係，闡述了複數的幾何加法與乘法。至此，複數理論才比較完整和系統...
歷史 主要內容 產生 共軛複數 複數的輻角。這裡，整數 m 稱為特徵值 λ 的 幾何重數，而 n 稱為 代數重數。這裡需要注意的是幾何重數與代數重數可以相等，但也可以不相等。一種最簡單...所有特徵值的幾何重數之和來確定。 分解方法矩陣的特徵分解 特徵分解 令...
基礎理論 分解方法有限維的，那么它的維數叫做λ 的幾何重數。 變換的主特徵矢量是模最大...相對的是特徵值的幾何重數：特徵值相對應的特徵空間（也就是λI &...A的一個特徵值λ的代數重數是λ作為A的特徵多項式的根的次數；換句話說，若...
定義 性質 套用