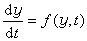正文
微分方程數值解法 連續系統的數學模型通常可用一組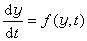
的一階常微分方程來描述，也可以寫成
這樣可以通過對f從時間t0至t1＝t0＋h積分,計算出經過一個計算步長h以後y的值,即 
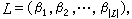
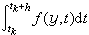這個積分式，所以此法也稱為數值積分法，它又可分為單步法和多步法。計算yk＋1隻需要用到yk和f(yk，tk)這一步的數據,稱為單步法。若完成這一步後還需要用到yk-1,f(yk-1,tk-1),yk-2，f(yk-2，tk-2),…等前幾步的數據，則稱為多步法。最常用的單步法是龍格庫塔法，最常用的多步法是阿旦姆斯法。一種改進的方法是變步長法，它能在仿真計算過程中自動估計誤差,並按精度要求不斷改變積分步長，因此對減少仿真計算時間有十分明顯的效果。 離散相似法 直接從傳遞函式或狀態方程轉換為適合在數字計算機上處理的離散傳遞函式或離散狀態方程的方法。它分為傳遞函式轉換法和狀態方程轉換法兩種。
傳遞函式轉換法 從系統的傳遞函式G(s)求出與它特性相似的離散傳遞函式G(z)的方法。其步驟是：①對輸入信號u(t)進行採樣，使之成為離散信號u(kT)，T為採樣周期，k＝0，1，2，…，②用信號重構器將 u(kT)恢復為連續信號╛t,③設信號重構器的傳遞函式為GH(s)，則G(z)＝z{GH(s)·G(s)}，式中z表示對括弧內的函式取Z變換。
為了保證仿真精度，要求採樣周期T 符合採樣定理,即T ≤π／&owega;m，其中&owega;m為輸入信號的最大角頻率。實際可採用的信號重構器都不可能完全恢復原來輸入的連續信號，所以會引起誤差。減少這種誤差的辦法是在信號重構器前或後增加一個補償器。另外還有一種直接利用s和z的替換關係由G(s)求出G(z)的方法，稱為替換法。如歐拉替換:
塔斯廷替換：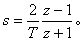
後者具有良好的計算穩定性和精度，又可用計算機自動進行這種轉換，因此套用較為廣泛。 狀態方程轉換法 從連續狀態方程經過離散化處理而求出與它特性相似的離散狀態方程的方法。離散化處理的過程與傳遞函式轉換法類似，因此同樣存在由信號重構器所造成的誤差，也可用補償的辦法來減少。如果能將輸入信號ut增廣為系統的狀態量，則可完全避免這部分誤差，此法稱為增廣矩陣法。
步驟 連續系統數字仿真的具體步驟是：①選擇合適的計算方法構成離散化的仿真模型。②選擇積分步長、積分時間。若採用浮點運算則不必選比例尺。③編制仿真程式框圖，按指定的語言編寫源程式。④將源程式和數據輸入計算機，上機求解。⑤記錄輸出的數據和圖形。
參考書目
G.A.科恩、J.V.韋特著，李仰東等譯：《連續系統數字仿真》，科學出版社，北京，1981。(G.A.Korn,J.V.Wait, Digital Continuous System Simulation, Prentice-Hall, Englewood Cliffs,N.J.,1978.)
John M.Smith, Mathematical Modelin gnd Digital Simulation for Enginerrs and Scientists, John Wiley and Sons, New York,1977.
