詳細介紹
有三個或三個以上支座的梁。連續梁有中間支座,所以它的變形和內力通常比單跨梁要小,因而在工程結構(如橋樑)和機件中套用很廣。
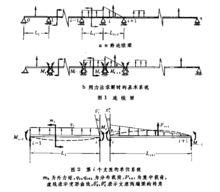
連續梁屬靜不定結構,可用力法求解其中的內力。具體方法是,對n跨連續梁(圖1a),將它在每個內部支座處斷開,變為鉸鏈連線,化成n根簡支梁,並以各支座處的彎矩M(i=1,2,…,n-1)為多餘的未知內力,就得到一個力法的基本系統(圖1b),而每個內部支座左右兩根梁形成一個單位系統(圖2)。根據轉角的連續條件,支座左右梁端的轉角應該相等,即
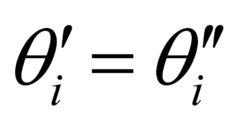 連續梁
連續梁運用單位載荷法計算該轉角,可得到力法的方程組。對於用同一材料製成的連續梁,這組方程為:
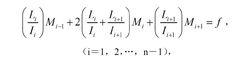 連續梁
連續梁式中L為第i個跨的跨距;I為第i個跨上的梁截面的慣性矩(見截面的幾何性質);fi是第i個支座的單位系統中各外載荷(集中力、分布力、力矩)的函式,外載荷給定後,它就是確定的。由於每個方程中含有三個支座力矩,所以這個方程組稱為三彎矩方程組,簡稱三彎矩方程。它的係數矩陣為三對角線矩陣。通過上述方法得到的三彎矩方程,便於在數學上求解(見變形分配法)。
 連續梁
連續梁簡史
最早得到三彎矩方程的是法國的B.P.E.克拉珀龍(1849)和H.貝爾托(1855),他們得到的方程組只適用於支座等高、跨距相等並受均布橫向載荷的連續梁。後來德國的H.舍夫勒等人將方程組推廣到支座不等高的情況。法國的J.布雷斯進一步又推廣到跨距不等並且載荷任意分布的情況。20世紀初,捷克斯洛伐克的K.A.恰利謝夫和美國的H.克羅斯為便於工程運用,又提出逐次近似的力矩分配法。50年代後期以來,發展出用有限元法解連續梁的多種標準程式。

