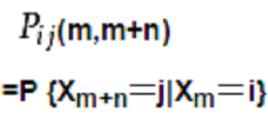定義
給定馬氏鏈於某時刻處於一狀態,再經若干時間將到達另一狀態的條件機率。設{X,n≥0}為離散時間馬爾可夫鏈。對任何m≥0,n≥1,i,j∈E,令
 轉移機率
轉移機率(m,m+n)=P {X=j|X=i}
稱p(m,m+n) 為鏈於m時在i,再經n步轉移到j的轉移機率,簡稱n步轉移機率。特別,一步轉移機率為p(m,m+1)。如果以p(m,m+n) 作為矩陣P (m,m+n)的第i行第j列元素,則P (m,m+n)稱為馬氏鏈的n步轉移陣。當E的有限集時,它是一個普遍方陣; 當E為可列無窮集時,它是一個有可列無窮多個行及列的矩陣。
轉移機率有如下基本性質:
對一切m,n,i,j有p(m,m+n) ≥0;
1.對一切m,n,i,j有p(m,m+n) ≥0;
 轉移機率
轉移機率2. 對一切m,n, i有 p(m, m+n)=1 。
一步轉移機率
對於馬氏鏈,描述其機率性質的最重要的概念是它在時刻m的一步轉移機率 .
1)定義 稱條件機率P{X(m+1)=j∣X(m)=i}(i,j∈I,I為狀態空間)為馬氏鏈{X(n),n≥o}在時刻m從狀態i到狀態j的一步轉移機率,記為
Pij(m),即有
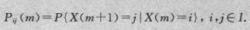 轉移機率
轉移機率2)轉移機率矩陣和隨機矩陣
定義 若I={0,1,2,......},稱矩陣
 轉移機率
轉移機率為轉移機率矩陣。
一步轉移機率Pij(m)表示在時刻m及X(m)取值i的條件下,在下一時刻
m+l,X(m+1)取值轉移到j的機率.
顯然,Pij(m)滿足以下兩個性質:
①o≤Pij(m)≤l,i∈I.
 轉移機率
轉移機率② Pij(m)≤l,i∈I.
轉移機率矩陣P(m)是一個具有非負元素的方陣,並且其各行元素之和都等
於1.凡是滿足上述兩個條件的矩陣,統稱為隨機矩陣或馬爾可夫矩陣.
k步轉移機率
一般地,還可以定義時刻m的k步轉移機率 .
定義:條件機率
 轉移機率
轉移機率稱為馬氏鏈{X(n)}在時刻m的k步轉移機率。稱矩陣
 轉移機率
轉移機率為k步轉移機率矩陣。
 轉移機率
轉移機率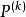 轉移機率
轉移機率k步轉移機率 (m)表示在時刻m及X(m)處於狀態i的條件下,經過k(k≥1)步到達狀態j的轉移機率.顯然 (m)也是一個隨機矩陣.
 轉移機率
轉移機率 轉移機率
轉移機率 轉移機率
轉移機率當k=1時,有 (m)= (m), (m)= P(m).
通常規定
 轉移機率
轉移機率套用舉例
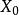 轉移機率
轉移機率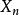 轉移機率
轉移機率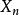 轉移機率
轉移機率 轉移機率
轉移機率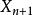 轉移機率
轉移機率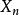 轉移機率
轉移機率例1 在只傳輸數字0和1的串聯繫統中(一般稱0-1傳輸系統),設每一級的傳真率(輸出與輸人數字相同的機率稱為系統的傳真率,相反情況稱為誤碼率)為p,誤碼率為q=1一p,並設一個單位傳輸一級: 是第一級的輸入, 是第n級的輸出(n≥1),那么{ ,n=0,1.2,…)是一個隨機過程,狀態空間I={0,1},且當 =i(i∈I為已知時, 所處狀態的機率分布只與 =i有關,而與時刻n以前所處的狀態無關,所以它是一個馬氏鏈,它的一步轉移機率和一步轉移機率矩陣分別為
 轉移機率
轉移機率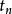 轉移機率
轉移機率例2 帶一維不可越壁的隨機遊動和帶吸收壁的隨機遊動,設線段[1,5]上有一個質點,假定它只能停留在1,2,3,4,5點,並且只能在t₁,t₂,…時刻發生隨機移動.移動規則是:移動前若在2,3,4點,則均以1/3的機率向左或向右移動一格或停留原處;若移動前在l點上,則以機率1移到2點;若移動前在5點上,則以機率1移到4點.以X(n)=i(i=1,2,3,4,5)表示質點在時刻 位於i點,則質點位置{X(n)}是一個馬氏鏈,狀態空間I={1,2,3,4,5).其轉移機率如圖所示 .
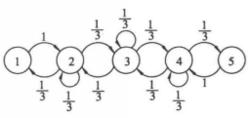 轉移機率示意
轉移機率示意轉移機率矩陣為
 轉移機率
轉移機率注意:狀態空間有多大,其轉移機率矩陣的階數就有多大.在本例遊動問題中,質點不能越過1和5點,稱為帶一維不可越壁的隨機遊動.改變遊動的機率法則(即轉移機率),就有不同類型的隨機遊動過程.
例如,在上述的隨機遊動中,質點一旦到達1或5就不動了,而其餘的遊動規則不變,則稱為帶吸收壁的隨機遊動.它也是一個馬氏鏈,其轉移機率矩陣為
 轉移機率
轉移機率其第1行是(1,0,0,0,0),第5行是(0,0,0,0,1),這是吸收壁的特徵.對於具有吸收壁的隨機遊動,當質點處於吸收壁時,稱過程處於吸收狀態,而稱其餘狀態過程處於非吸收狀態.
注意:i為吸收狀態,若且唯若對於任意n,有Pij(n)=1.
例3 (排隊模型)設服務系統由一個服務員和只可以容納2個人的等待室組成,服務規則是先到先服務(FCFS),後來者需在等待室依次排隊,假定一個需要服務的顧客到達系統時發現系統內已有3個顧客(一個正在接受服務,二個在等候室排隊),則該顧客即離去(損失制).設時間間隔Δt有一個顧客進入系統的機率為q,一個原來被服務的顧客離開系統(即服務完畢)的機率為p,又設當Δt充分小時,在這段時間間隔內多於一個顧客進入或離開系統實際上是不可能的,再設有無顧客來到與服務是否完畢是相互獨立的,現用馬氏鏈來描述這個服務系統.
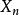 轉移機率
轉移機率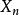 轉移機率
轉移機率設 =X(nΔt)表示時刻nΔtt時系統內的顧客數即系統的狀態,{ ,n=0,1,2,…)是一隨機過程,狀態空間I={0,1,2,3},仿前分析,它是一個馬氏鏈.現計算此馬氏鏈的一步轉移機率 .
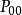 轉移機率
轉移機率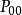 轉移機率
轉移機率為在系統內沒有顧客的條件下,經△t後仍沒有顧客的機率(此處是條件機率,以下同), =1一q.
 轉移機率
轉移機率 轉移機率
轉移機率為系統內沒有顧客的條件下,經△t以後進入一個顧客的機率, =q.
 轉移機率
轉移機率 轉移機率
轉移機率為系統內恰有一個顧客正在接受服務的條件下,經△t後系統內無人的機率,它等於在△t間隔內顧客因服務完畢而離去,且無人進入系統的機率, =p(1一q).
 轉移機率
轉移機率 轉移機率
轉移機率為系統內恰有一個顧客的條件下,在△t間隔內因服務完畢而離去,而另一個顧客進入系統;或者正在接受服務的顧客繼續要求服務,且無人進入系統的機率, =pq+(1-p)(1-q).
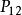 轉移機率
轉移機率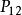 轉移機率
轉移機率為正在接受服務的顧客繼續要求服務,且△t間隔內另一個顧客進入系統的機率, =(1一p)q.
 轉移機率
轉移機率 轉移機率
轉移機率為正在接受服務的顧客繼續要求服務,且在△t間隔內有2個顧客進入系統的機率,由假設可知,後者實際上是不可能發生的,故有 =0.
類似地,有
 轉移機率
轉移機率 轉移機率
轉移機率= =p(1一q),
 轉移機率
轉移機率=pq+(1一p)(1一q),
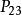 轉移機率
轉移機率 轉移機率
轉移機率=q(1一p), =0(|i﹣j∣≥2).
 轉移機率
轉移機率 轉移機率
轉移機率為一個顧客因服務完畢離去且另一個顧客進入系統,或者無人離開系統的機率, =pq+(1一p).
於是該馬氏鏈的一步轉移機率矩陣為
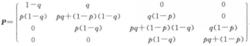 轉移機率
轉移機率