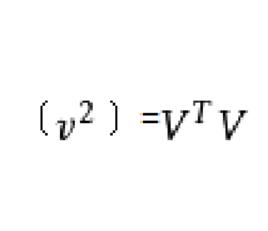公式概念
為了明確解釋變數和隨機誤差各產生的效應是多少,統計學上把數據點與它在回歸直線上相應位置的差異稱為殘差,把每個殘差平方之後加起來 稱為殘差平方和,它表示隨機誤差的效應。一組數據的殘差平方和越小,其擬合程度越好。
計算
按定義,殘差平方和應為
等精度測量:
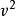 殘差平方和
殘差平方和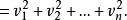 殘差平方和
殘差平方和﹝ ﹞
非等精度測量:
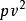 殘差平方和
殘差平方和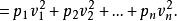 殘差平方和
殘差平方和﹝ ﹞
 殘差平方和
殘差平方和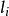 殘差平方和
殘差平方和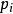 殘差平方和
殘差平方和式中 是測量數據 的殘差, 為相應的權。在一般情況下
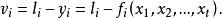 殘差平方和
殘差平方和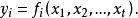 殘差平方和
殘差平方和式中, 為直接測量參數的估計值。
對於線性參數,殘差為
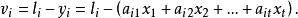 殘差平方和
殘差平方和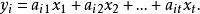 殘差平方和
殘差平方和式中
用矩陣形式表示的殘差平方和為
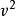 殘差平方和
殘差平方和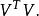 殘差平方和
殘差平方和﹝ ﹞=
線性參數測量數據的殘差平方和可進一步寫成
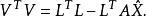 殘差平方和
殘差平方和(對等精度測量)
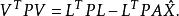 殘差平方和
殘差平方和(對非等精度測量)
式中符號的意義與前面相應的的符號一致。
以上給出了殘差平方和的一般形式。在具體解算時,從計算方便考慮,對不同的解算方法,殘差平方和的計算各有相應的具體方法。
性質
解釋變數與殘差平方和
殘差平方和RSS具有以下性質:
性質1 只有常數項沒有其他解釋變數的回歸方程的RSS和TSS相等,其決定係數為0。
性質2 增加解釋變數必然導致RSS減小。因此,如果想降低RSS,只要在回歸方程中儘可能地加入解釋變數就能達到目的。
性質3 包含常數項全部解釋變數的個數K等於樣本數n時,RSS為0,決定係數為1。
F檢驗和t檢驗之間的關係
在一些場合t檢驗不僅可以進行雙側檢驗,也可以進行單側檢驗。而F檢驗沒有單側和雙側的區別。當進行雙側檢驗的時候兩種檢驗的P值相同。
分布
機率分布
 殘差平方和
殘差平方和殘差帶權平方和除以單位權方差服從 分布。即
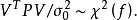 殘差平方和
殘差平方和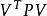 殘差平方和
殘差平方和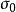 殘差平方和
殘差平方和式中自由度f就是平差中多餘觀測數。由於 , ,f對於一個平差系統是不變數,與具體採用的平差方法無關。
數學期望和方差
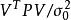 殘差平方和
殘差平方和易知 的數學期望為
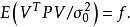 殘差平方和
殘差平方和由此可知
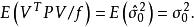 殘差平方和
殘差平方和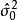 殘差平方和
殘差平方和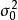 殘差平方和
殘差平方和即單位權方差 為 的無偏估計。
且
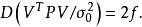 殘差平方和
殘差平方和則有
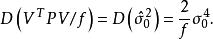 殘差平方和
殘差平方和或
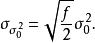 殘差平方和
殘差平方和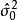 殘差平方和
殘差平方和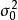 殘差平方和
殘差平方和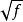 殘差平方和
殘差平方和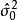 殘差平方和
殘差平方和即方差估計 的標準差與 成正比與 成反比。可見自由度f 愈小,方差估計 的精度就愈差。
機率表達式
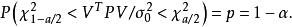 殘差平方和
殘差平方和或
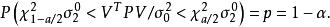 殘差平方和
殘差平方和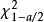 殘差平方和
殘差平方和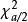 殘差平方和
殘差平方和 殘差平方和
殘差平方和 殘差平方和
殘差平方和分位值 , 以自由度f和顯著水平 可由 分布表中查得。