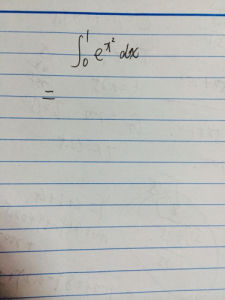簡介
對於一些積分,如果不引入新的函式,那么那些積分就有可能不可積,而且這種情況還會經常遇到.因此對於一些常見的超越積分,一般都定義了相關的新函式。
常見
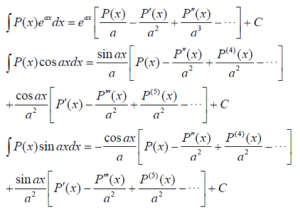超越函式積分1.∫e^(ax^2)dx(a≠0)
2.∫(sinx)/XDX
3.∫(cosx)/xdx
4.∫sin(x^2)dx
5.∫cos(x^2)dx
6.∫x^n/lnxdx(n≠-1)
7.∫lnx/(x+a)dx(a≠0)
8.∫(sinx)^zdx(z不是整數)
9.∫dx/√(x^4+a)(a≠0)
10.∫√(1+k(sinx)^2)dx(k≠0,k≠-1)
11.∫dx/√(1+k(sinx)^2)(k≠0,k≠-1)
以後凡是看到以上形式的積分,不要繼續嘗試,因為以上積分都已經被證明了為不可積積分.但是要注意的是,雖然以上積分的原函式不是初等函式.
但並不意味著他們的定積分不可求,對於某些特殊點位置的定積分還是有可能算出來的,只不過不能用牛頓-萊布尼茨公式罷了!
比如∫[0,+∞)e^(-x^2)dx=√π/2,此處的積分值就是用二重積分和極限夾逼的方法得出的,而且只能算出(-∞,+∞)或是(0,+∞)上的值,其他的值只能用數值方法算出近似值。
