超球面介紹
1.定義
 超球面
超球面 超球面
超球面高於2維的球面稱為 超球面。中心位於原點且半徑為單位長度的 維球面稱為單位 n維球面,記為 。用符號來表示,就是:
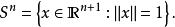 超球面
超球面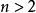 超球面
超球面 超球面
超球面超球面是 n維球體( )的表面或邊界,是 維流形的一種 。
 超球面
超球面 超球面
超球面 超球面
超球面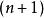 超球面
超球面 超球面
超球面 超球面
超球面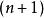 超球面
超球面 超球面
超球面對於任何自然數,半徑為的維球面定義為維歐幾里得空間中到某個定點的距離等於常數的所有點的集合,其中 可以是任何正的實數。它是維空間內的維流形。特別地:
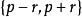 超球面
超球面1) 0維球面是直線上的兩個點;
2) 1維球面是平面上的圓;
3) 2維球面是三維空間內的普通球面;
4)3維球面是四維空間內的球面。
2.(n+1)維空間中的歐幾里得坐標
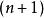 超球面
超球面 超球面
超球面 超球面
超球面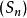 超球面
超球面維空間中的點:定義了一個維球面,由以下方程表示:
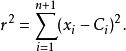 超球面
超球面 超球面
超球面 超球面
超球面其中是中心點,是半徑。
 超球面
超球面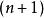 超球面
超球面 超球面
超球面 超球面
超球面 超球面
超球面 超球面
超球面以上的維球面在維空間中存在,是維流形的一個例子。半徑為的維球面的體積形式由下式給出:
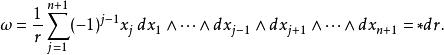 超球面
超球面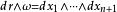 超球面
超球面其中*是霍奇星運算元。因此,。
3.超球體
 超球面
超球面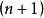 超球面
超球面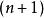 超球面
超球面由維球面所包圍的體積,稱為維球體。如果把球體的表面包括在內,則維球體是封閉的,否則是開放的。
特別地:
1) 1維球體,是一個線段,是0維球面的內部。
2) 2維球體,是一個圓盤,是圓(1維球面)的內部。
3) 3維球體,是一個普通的球體,是球面(2維球面)的內部。
4) 4維球體,是3維球面的內部。
超球體體積
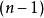 超球面
超球面 超球面
超球面維球面所包圍的體積( 維球體的體積)由以下公式給出:
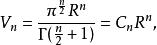 超球面
超球面 超球面
超球面 超球面
超球面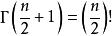 超球面
超球面 超球面
超球面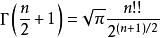 超球面
超球面 超球面
超球面其中 是伽瑪函式。對於偶數 , ;對於奇數 , ,其中 表示雙階乘。
 超球面
超球面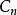 超球面
超球面由此可以推出,對於給定的 ,常數 的值為:
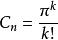 超球面
超球面1) (對於偶數 n=2 k),
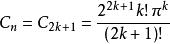 超球面
超球面2) (對於奇數 n=2 k+1)。
這個(n-1)維球面的表面積是:
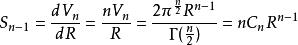 超球面
超球面n維球面的表面積和體積之間有以下的關係:
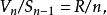 超球面
超球面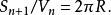 超球面
超球面從此可以推導出遞推關係:
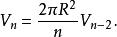 超球面
超球面這些公式也可以直接從 n維球坐標系中的積分推出。
例子
 超球面
超球面 超球面
超球面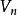 超球面
超球面對於較小的 ,半徑為 維球體的的體積 為如下:
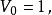 超球面
超球面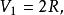 超球面
超球面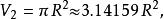 超球面
超球面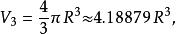 超球面
超球面 超球面
超球面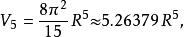 超球面
超球面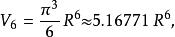 超球面
超球面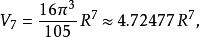 超球面
超球面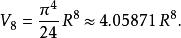 超球面
超球面 超球面
超球面 超球面
超球面但當 趨於無窮大時,趨於0。
 超球面
超球面 超球面
超球面 超球面
超球面 超球面
超球面 超球面
超球面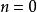 超球面
超球面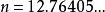 超球面
超球面如果維度不限於整數,那么維球面的體積就是的連續函式,它的極大值位於,體積為。當或時,體積為1。
 超球面
超球面 超球面
超球面單位維球面的外切超正方體的邊長為2,因此體積為2;當維度增加時,維球面的體積與外切於它的超正方體的體積之比單調減少。
超球坐標系
 超球面
超球面 超球面
超球面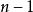 超球面
超球面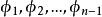 超球面
超球面 超球面
超球面可以定義維空間內的坐標系統,與3維空間內的球坐標系類似,由徑向坐標 和 個角度坐標 組成。如果 是笛卡兒坐標系,那么我們可以定義 :
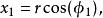 超球面
超球面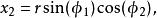 超球面
超球面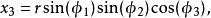 超球面
超球面 超球面
超球面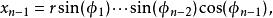 超球面
超球面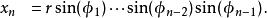 超球面
超球面從中可以推出逆變換的公式:
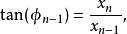 超球面
超球面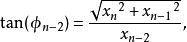 超球面
超球面 超球面
超球面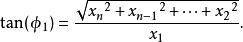 超球面
超球面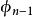 超球面
超球面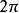 超球面
超球面 超球面
超球面注意最後一個角 的值域為 ,而其它角的值域為 。這個值域覆蓋了整個球面。
 超球面
超球面維空間內的體積元素可以從變換的雅可比行列式得出:
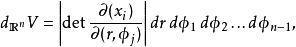 超球面
超球面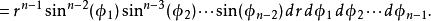 超球面
超球面以上n維球體的體積方程可以通過積分來重新得出:
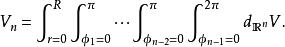 超球面
超球面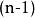 超球面
超球面維球面的體積元素是2維球面的面積元素的推廣,由以下公式給出:
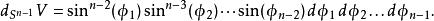 超球面
超球面