介紹
n維球面是普通的球面在任意維度的推廣。它是( n+1)維空間內的 n維流形。特別地，0維球面就是直線上的兩個點，1維球面是平面上的圓，2維球面是三維空間內的普通球面。高於2維的球面有時稱為 超球面。中心位於原點且半徑為單位長度的 n維球面稱為 單位n維球面，記為 S。用符號來表示，就是：
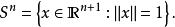n維球面n維球面是( n+1)維球體的表面或邊界，是 n維流形的一種。對於 n≥2， n維球面是單連通的 n維流形，其曲率為正的常數。
描述
對於任何自然數 n，半徑為 r的 n維球面定義為( n+1)維歐幾里得空間中到某個定點的距離等於常數 r的所有點的集合，其中 r可以是任何正的實數。它是( n+1)維空間內的 n維流形。特別地：
•0維球面是直線上的兩個點{p−r,p+r}；
•1維球面是平面上的圓；
•2維球面是三維空間內的普通球面；
•3維球面是四維空間內的球面。
空間中的歐幾里得坐標
( n+ 1)維空間中的點：( x、 x、 x、……、 x)定義了一個 n維球面( S)，由以下方程表示：
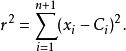n維球面其中 C是中心點， r是半徑。
以上的 n維球面在( n+1)維空間中存在，是 n維流形的一個例子。半徑為{\displaystyle r}的 n維球面的體積形式ω由下式給出：
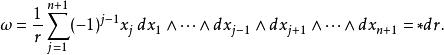n維球面
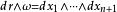n維球面其中*是霍奇星運算元。因此， 。
n維球體
由 n維球面所包圍的體積，稱為( n+1)維球體。如果把球體的表面包括在內，則( n+1)維球體是封閉的，否則是開放的。
特別地：
•1維球體，是一個線段，是0維球面的內部。
•2維球體，是一個圓盤，是圓（1維球面）的內部。
•3維球體，是一個普通的球體，是球面（2維球面）的內部。
•4維球體，是3維球面的內部。
球極平面投影
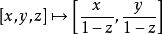n維球面就像三維空間中的二維球面可以通過球極平面投影映射到二維平面上一樣，一個n維球面也可以通過球極平面投影的n維形式映射到n維超平面。例如，半徑為1的二維球面上的點 [x,y,z]映射到xy平面上的點 。也就是說：
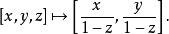n維球面
n維球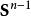面
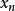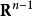n維球面
n維球面類似地，半徑為1的n維球面 的球極平面投影映射到垂直於 軸的n-1維超平面 ：
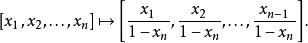n維球面參見
•共形幾何
•同調球
•球的同倫群
•同倫球
•雙曲群
•超正方體
•反演幾何
•正交群
•莫比烏斯變換
