概念
賦值環(valuation ring)是一種特殊的局部環。也是重要的交換環類。交換環R稱為賦值環,是指它滿足以下等價條件之一:
1.對任意a,b∈R,恆有a∈Rb或b∈Ra,換言之,必有a整除b或b整除a。
2.R的所有理想(對於包含關係)組成線性序集。
3.R是局部環且任意有限生成理想是主理想。滿足條件3的環也稱為貝祖特環。
賦值環是交換的特殊序列。它與戴德金環有密切的關係。事實上,交換諾特局部整環是賦值環若且唯若它是戴德金環。賦值環上的模具有良好的分解性質,馬特利斯(Matlis,E.)於1957年證明:賦值環R上任意有限生成模M的內射包E(M)是有限個不可分解內射模的直和,或等價於M有有限哥爾迪維數。賦值環R上任意有限表示模是循環表示模的直和,從而推廣了卡普蘭斯基(Kaplansky,I.)的工作。
環
環是對並與差運算封閉的集類,測度論中重要概念之一。設F是Ω上的一個非空集類。如果它對集的並及差運算封閉,即對任何A,B∈F,都有A∪B∈F,A\B∈F,則稱F為Ω上的環。例如,若F是由實直線R上任意有限個左開右閉的有限區間的並集:
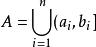 賦值環
賦值環的全體構成的集類,則F是R上的一個環.環也是對於交與對稱差運算封閉的集類,並按這兩種運算成為布爾環。要把R上的勒貝格測度和勒貝格-斯蒂爾傑斯測度以及相應的積分理論推廣到更一般的集合上,就需要做一系列奠基工作,其中之一是建立一些特殊的集類並研究其性質。環以及半環、σ環、代數、σ代數等重要集類正是為了這一目的而引入的。
局部環
它和半局部環分別是完全準素環和半準素環概念的推廣。環R(≠0)中,若不可逆元(即非單位)集A對於加法是封閉的,則R稱為局部環。以下性質是等價的:
1.R是局部環。
2.R中不可逆元的集A是(雙邊)理想。
3.A是極大左(右)理想。
4.對於任意r∈R,r或1-r必是左(右)可逆元。
5.R的雅各布森根J(R)是極大左(右)理想。
6.R/J(R)是除環。
7.J(R)=A={x∈R|Rx≠R}(x稱為非生成子)。
若R/R(J)是半單的,則稱R是半局部的。局部環的概念對於模的分解性質十分重要。對於任意R模M,若M的自同態環End(M)是局部的,則M是不可分解的.反之,若M是不可分解且是內射的,則End(M)是局部環。東屋五郎(Azumaya,G.)曾利用局部環的概念,把古典的克魯爾-銳瑪克-施密特定理推廣為項數可以是無窮的情形。局部環也具有特殊的同調性質。卡普蘭斯基(Kaplansky,I.)於1958年證明:對於局部環R,任意R投射模是R自由的。
環論
抽象代數學的主要分支之一。它是具有兩個運算的代數系。在非空集合R中定義加法“+”和乘法“·”運算,使得R中任意元a,b,c適合條件:
1.R對加法為交換群,稱為R的加法群,記為(R,+);
2.R對乘法適合結合律,即(R,·)是半群,稱為R的乘法半群;
3.乘法對加法的左、右分配律成立,即a·(b+c)=a·b+a·c (左分配律),(b+c)·a=b·a+c·a (右分配律);
則稱R為結合環,簡稱環(通常a·b寫為ab)。它是環論研究的主要對象。環論起源於19世紀關於實數域的擴張與分類,以及戴德金(Dedekind,J.W.R.)、哈密頓(Hamilton,W.R.)等人對超複數系的建立和研究。韋德伯恩(Wedderburn,J.H.M.)於1907年給出的結構定理給出代數研究的模式,也成為環結構研究的模式。20世紀20-30年代,諾特(Noether,E.)建立了環的理想理論,阿廷(Artin,E.)又將代數結構定理推廣到有極小條件的環。同時,對非極小條件的環,馮·諾伊曼(von Nenmann,H.)建立了正則環理論,相繼蓋爾范德(Гельфанд,И.М.)創立了賦值環,克魯爾(Krull,W.)建立了局部環理論,以及哥爾迪(Goldie,A.W.)完善了極大條件環理論。
20世紀40年代,根論迅速發展,尤其是雅各布森(Jacobson,N.)於1945年引入的被稱為雅各布森根的概念後,建立了本原環理論、半本原環的結構定理與本原環的稠密性定理,完善和深化了不帶附加條件環的理論。20世紀50年代中期,阿密蘇(Amitsur,S.A.)、庫洛什(Kurosh,A.)創立了根的一般理論,環論已趨完善。
另一方面,由群表示研究的影響,產生模、群環與分次環的理論。20世紀20年代初,諾特引入了模的概念,並研究模對有限群表示的作用與環結構之間的關係,用模的語言去刻畫環,特別是20世紀50年代以後,同調代數的迅速發展,使環的理論進入更高層次雖然,早在1854年,凱萊(Cayley,A.)就引入了群代數,然而,它的研究是從20世紀30年代開始直到60—70年代,受群表示論與環的理論的推動才蓬勃發展起來的。20世紀70年代後,由於分次代數的推動,群代數進入新的階段——交叉積的研究。分次環與模發展的另一動力是交換代數幾何中射影代數簇,20世紀70年代以來,由於非交換代數幾何及群表示論的推動,環論已進入一個新的階段。
戴德金環
理想可以惟一素分解的環。最重要的例子是:數域的整數環、光滑曲線的坐標環。按定義,滿足下述三條件的整環R稱為戴德金環:
1.R是諾特環。
2.R的真素理想均為極大理想。
3.R在其商域F(≠R)中是整閉的。
事實上,對每個戴德金環R及其商域F,總存在F的離散素除子集S使{F,S}為普通算術域而R為S整數環。整環R(≠其商域F)為戴德金環若且唯若其每個真理想均為極大理想的積;也等價於其每個分式理想均可逆,即分式理想全體構成群。戴德金環R在其商域F的有限可分擴張E中的整閉包R也為戴德金環,且E是R的商域。
