定義
 局部環
局部環 局部環
局部環 局部環
局部環 局部環
局部環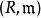 局部環
局部環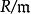 局部環
局部環 局部環
局部環設為交換含麼環。若僅有一個極大理想,則稱(或)為 局部環。域稱為的 剩餘域。
 局部環
局部環若中僅有有限個極大理想,則稱之為 半局部環。
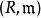 局部環
局部環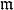 局部環
局部環 局部環
局部環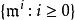 局部環
局部環 局部環
局部環 局部環
局部環一個局部環上帶有一個自然的 -進拓撲,使得成為拓撲環;其開集由生成。當 為諾特環時,可證明為豪斯多夫空間,且所有理想皆是閉理想。
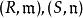 局部環
局部環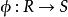 局部環
局部環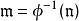 局部環
局部環設為局部環,環同態被稱為 局部同態,若且唯若。
例子
域是局部環。
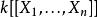 局部環
局部環 局部環
局部環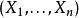 局部環
局部環形式冪級數環是局部環,其中是個域。極大理想是。
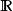 局部環
局部環 局部環
局部環取係數在或上,原點附近收斂半徑為正的冪級數,它構成一個局部環,極大理想表法同上。
凡賦值環皆為局部環。
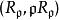 局部環
局部環 局部環
局部環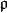 局部環
局部環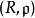 局部環
局部環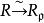 局部環
局部環設為任意交換環,為素理想,則相應的局部化是局部環;這也是局部環套用的主要場合。若已是局部環,則。
局部環的商環仍是局部環。
動機與幾何詮釋
 局部環
局部環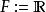 局部環
局部環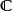 局部環
局部環 局部環
局部環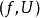 局部環
局部環 局部環
局部環 局部環
局部環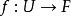 局部環
局部環局部環意在描述一個點附近的函式“芽”。設為拓撲空間,或,且。考慮所有資料,其中是的一個開鄰域,而是連續函式。引入等價關係:
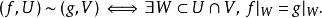 局部環
局部環 局部環
局部環 局部環
局部環且是的開鄰域。
 局部環
局部環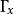 局部環
局部環 局部環
局部環 局部環
局部環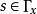 局部環
局部環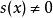 局部環
局部環 局部環
局部環 局部環
局部環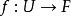 局部環
局部環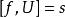 局部環
局部環 局部環
局部環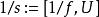 局部環
局部環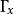 局部環
局部環 局部環
局部環 局部環
局部環換言之,若兩個函式在附近一致,則視之等同。上述等價類在逐點的加法及乘法下構成一個環,其元素稱作在的 連續函式芽,它體現了連續函式在附近的行為。若滿足,則存在一個的開鄰域及連續函式,使得且恆非零,因此可定義乘法逆元。於是是局部環,其唯一的極大理想是所有在點取零的函式,剩餘域則是。
類似想法可施於微分流形、解析流形或複流形,稍作修改後亦可推廣至代數簇與概形。
在代數幾何與復幾何中,假設適當的有限性條件(例如凝聚性), 若一陳述對某一點的芽成立,則在該點的某個開鄰域上皆成立;就此而論,局部環集中表現了一點附近的 局部性質。
在交換代數中,局部化的技術往往可將問題化約到局部環上;因此交換代數的許多定義與結果都落在局部環的框架內。
非交換的情形
 局部環
局部環一個含么環被稱作 局部環,若且唯若它滿足下述等價條件:
R 僅有一個極大左理想。
R 僅有一個極大右理想。
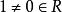 局部環
局部環,且任兩個非可逆元的和仍為非可逆元。
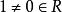 局部環
局部環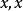 局部環
局部環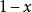 局部環
局部環,且對任何元素或必有一者可逆。
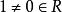 局部環
局部環 局部環
局部環,若中某個有限和是可逆元,則其中某項必可逆。
當上述任一性質成立,則下述三者等同:
•R 的唯一極大左理想。
•R 的唯一極大右理想。
•R 的Jacobson根。
對於交換環,上述定義化為交換局部環的原始定義。
