基本介紹
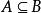 整閉整環
整閉整環 整閉整環
整閉整環 整閉整環
整閉整環命題1令是環,在上整。
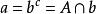 整閉整環
整閉整環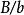 整閉整環
整閉整環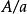 整閉整環
整閉整環i) 如果b是B的理想,,那么在上整。
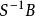 整閉整環
整閉整環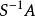 整閉整環
整閉整環ii) 如果S是A的乘法封閉子集,那么在上整。
命題(1)的ii)可以加強為:
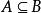 整閉整環
整閉整環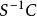 整閉整環
整閉整環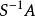 整閉整環
整閉整環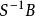 整閉整環
整閉整環命題2 令是環,C是A在B中的整閉包,令S是A的一個乘法封閉子集,那么是在中的整閉包。
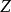 整閉整環
整閉整環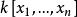 整閉整環
整閉整環定義 一個整環叫作 整閉的(沒有限制條件),如果它在它的分式域中是整閉的。例如,是整閉的,任何唯一因子分解整環都是整閉的,特別,域上的多項式環是整閉的 。
相關性質
整閉性是局部性質:
命題3 令A是一個整環,那么下列斷言是等價的:
i) A是整閉的;
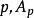 整閉整環
整閉整環ii) 對每個素理想是整閉的;
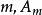 整閉整環
整閉整環iii)對每個極大理想是整閉的。
 整閉整環
整閉整環 整閉整環
整閉整環 整閉整環
整閉整環 整閉整環
整閉整環引理1 令C是A在B中的整閉包,表示在C中的擴理想,那么在B中的整閉包是的根(因此在加法和乘法之下是封閉的)。
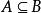 整閉整環
整閉整環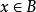 整閉整環
整閉整環 整閉整環
整閉整環 整閉整環
整閉整環 整閉整環
整閉整環 整閉整環
整閉整環 整閉整環
整閉整環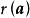 整閉整環
整閉整環命題4 令是整環,A是整閉的,在A的理想上整,那么在A的分式域K上代數,而且如果在K上的極小多項式是,那么位於中。
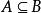 整閉整環
整閉整環 整閉整環
整閉整環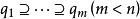 整閉整環
整閉整環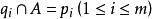 整閉整環
整閉整環 整閉整環
整閉整環 整閉整環
整閉整環 整閉整環
整閉整環定理(“下降定理”)令是整環,A是整閉,B在A上整,令是A的素理想鏈,是B的素理想鏈,使得,那么鏈可以擴充為鏈,使得。
 整閉整環
整閉整環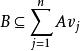 整閉整環
整閉整環命題5令A是一個整閉的整環,K是它的分式域,L是K的一個有限可分代數擴張,B是A在L中的整閉包,那么存在L在K上的基,使得。
Dedekind環
稱環A為Dedekind環是說A滿足下面的條件(1)一(3) 。
(1) A為Noether環;
(2) A為整閉整環;
(3) 除0以外的A的素理想(ideal)均為極大理想。
這裡我們來解釋一下所用術語的意思。A為Noether環是說A滿足下述條件(1)。
(1) A的任意理想均為有限生成。
這個條件與下述(2)一(4)中任一個均等價。
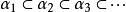 整閉整環
整閉整環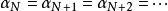 整閉整環
整閉整環(2) 設為A的理想的遞增序列,則存在N使得
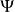 整閉整環
整閉整環 整閉整環
整閉整環 整閉整環
整閉整環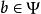 整閉整環
整閉整環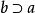 整閉整環
整閉整環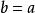 整閉整環
整閉整環(3) 設為A的理想組成的非空集合,則存在屬於的滿足條件“如果且,則”.
(4) 有限生成A模的子模也是有限生成的。
稱A為 整環是說A為非零環,而且滿足條件
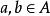 整閉整環
整閉整環 整閉整環
整閉整環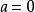 整閉整環
整閉整環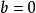 整閉整環
整閉整環對於,若則或或.
當A為環B的子環時,稱B的元x在A上整是說x滿足某個A係數方程
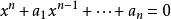 整閉整環
整閉整環 整閉整環
整閉整環 整閉整環
整閉整環(,為自然數)
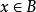 整閉整環
整閉整環 整閉整環
整閉整環環B中所有在A上整的元全體{ |在A上整}構成了B的子環,稱之為A在B中的 整閉包。當A為整環時,A在A的分式域中的整閉包被簡單地稱為A的整閉包,當A與A的整閉包相同時,則說A為 整閉。
 整閉整環
整閉整環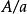 整閉整環
整閉整環稱環A的理想為 素理想是說,剩餘環為整環,這個條件等價於滿足下面的條件(1),(2)。
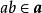 整閉整環
整閉整環 整閉整環
整閉整環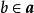 整閉整環
整閉整環(1)若,則或或;
 整閉整環
整閉整環(2)。
 整閉整環
整閉整環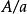 整閉整環
整閉整環稱A的理想為極大是說剩餘環為域,這個條件等價於滿足下面的條件(1),(2)。
 整閉整環
整閉整環 整閉整環
整閉整環(1)包含的A的理想只有A或是自己;
 整閉整環
整閉整環(2)。
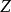 整閉整環
整閉整環極大理想是素理想,反過來不成立,例如的素理想0 。

