費馬引理

費馬（Fermat）引理是實分析中的一個定理，以皮埃爾·德·費馬命名。通過證明函式的每一個極值都是駐點（函式的導數在該點為零），該定理給出了一個求出可微函式的最大值和最小值的方法。因此，利用費馬引理，求函式的極值的問題便化為解方程的問題。需要注意的是，費馬引理僅僅給出了函式在某個點為極值的必要條件。也就是說，有些駐點可以不是極值，它們是拐點。要想知道一個駐點是不是極值，並進一步區分極大值和極小值，我們需要分析二階導數（如果它存在）。當該點的二階導數大於零時，該點為極小值點；當該點的二階導數小於零時，該點為極大值點。若二階導數為零，則無法用該法判斷，需列表判斷。

基本信息

• 中文名稱：費馬引理
• 外文名：Fermat's theorem
• 別稱：Fermat引理
• 提出者：皮埃爾·德·費馬
• 套用學科：數學
• 適用領域範圍：微積分

引理簡介

費馬引理

一個引理可用於證明多個結論。數學中存在很多著名的引理，這些引理可能對很多問題的解決有幫助。例如歐幾里得引理，烏雷松引理，德恩引理，法圖引理，高斯引理，中山引理，龐加萊引理，里斯引理和佐恩引理等。
引理和定理沒有嚴格的區分。

內容陳述

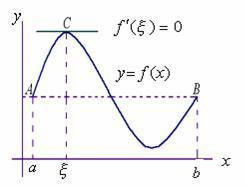
函式f(x)在點ξ的某鄰域U（ξ)內有定義，並且在ξ處可導，如果對於任意的x∈U（ξ)，都有f(x)≤f(ξ)(或f(x)≥f(ξ))，那么f'（ξ）=0。

證明方法

方法1	方法1
方法2	方法2

相關定理

費馬大定理費馬大定理，又被稱為“費馬最後的定理”，由法國數學家費馬提出。
它斷言當整數n>2時，關於x,y,z的方程x^n+y^n=z^n沒有正整數解。
被提出後，經歷多人猜想辯證，歷經三百多年的歷史，最終在1995年被英國數學家安德魯·懷爾斯證明。