緒論
費曼(R.F.Feynman)-海爾曼(H.Hellma-nn)定理又稱費曼一海爾曼關係，發表於30年代後期。它套用極廣，既可用作理論分析，又可用於具體計算。凡用維里定理可以處理的問題，肯定都可以用費曼一海爾曼定理(以下簡稱F-H定理)來處理。H-F定理的用處遠在維里定理之上，在量子力學教材中占有一席地位。
概念
費曼–海爾曼定理分別被不同的物理學家獨立地證明過，包括Paul Güttinger（1932）、泡利（1933）、海爾曼（1937）以及費曼（1939）。
該定理的表達式如下：
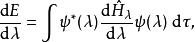費曼-海爾曼定理式中
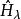費曼-海爾曼定理
費曼-海爾曼定理表示依賴於連續變化的參變數的哈密頓量；
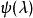費曼-海爾曼定理 費曼-海爾曼定理是該哈密頓量的本徵函式，通過哈密頓量間接依賴於；
費曼-海爾曼定理為能量，即哈密頓量的本徵值；
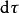費曼-海爾曼定理為積分微元。上述積分在全空間進行。
特例
對於隨時間變化的波函式的費曼–海爾曼定理來說，因為一個一般的隨時間變化的波函式滿足含時薛丁格方程，所以費曼–海爾曼定理 不再適用。
但是，該波函式滿足以下關係：
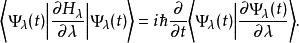費曼-海爾曼定理其中ψ滿足：
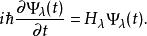費曼-海爾曼定理理論證明
以下證明只依賴於薛丁格方程，以及對於λ和t求偏導時，可以互換順序的假設。
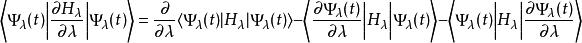費曼-海爾曼定理
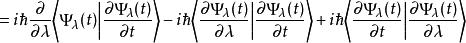費曼-海爾曼定理
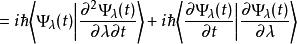費曼-海爾曼定理
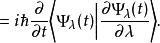費曼-海爾曼定理