定義
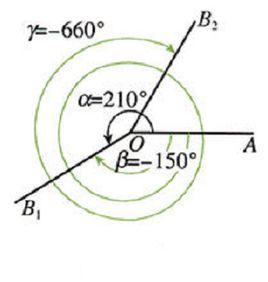
在平面內角的終邊繞角的頂點旋轉時,可以有兩個不同的方向,一個是逆時針方向,一個是順時針方向,沿逆時針方向旋轉生成的角規定為 正角;沿順時針方向旋轉生成的角則規定為 負角,圖1中β,γ皆為負角。
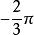 負角
負角正角的大小用正實數表示,如1108°、41弧度等,負角的大小用負實數表示,如-19.7°、 弧度等。
當角的終邊沒有作任何旋轉時,仍和始邊重合,這時也認為形成了一個角,並把它叫做零角。
負角的角度、弧度值皆為負(-180度=-π弧度)。
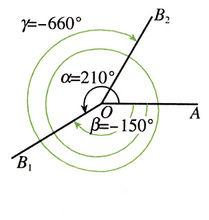 正角與負角的圖例
正角與負角的圖例負角的弧度制
弧度制是一種度量角的制度,它的單位是:等於半徑長的圓弧所對的圓心角叫做一弧度的角,規定正角的弧度數為正數,負角的弧度數為負數,零角的弧度數為零。
 負角
負角任一已知角 的弧度數的絕對值是:
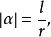 負角
負角 負角
負角 負角
負角其中 為圓心角 所對的弧長,r為圓半徑。
例如,圓周角的弧度數為:
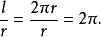 負角
負角當採用弧度制度量角的大小以後,那么角的大小(正或負)與實數之間就建立起一一對應關係。那么作為角的三角函式,就可以看成實數的三角函式加以研究。 ·
負角的三角函式
 負角
負角 負角
負角 負角
負角| 函式 | 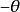 負角 負角 | 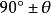 負角 負角 | 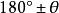 負角 負角 | 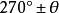 負角 負角 |
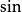 負角 負角 | 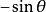 負角 負角 |  負角 負角 | 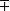 負角 負角 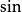 負角 負角 | 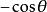 負角 負角 |
 負角 負角 |  負角 負角 | 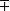 負角 負角 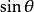 負角 負角 | 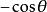 負角 負角 | 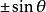 負角 負角 |
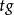 負角 負角 | 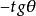 負角 負角 | 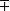 負角 負角 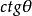 負角 負角 | 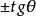 負角 負角 | 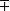 負角 負角 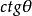 負角 負角 |
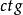 負角 負角 | 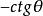 負角 負角 |  負角 負角 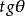 負角 負角 | 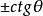 負角 負角 | 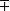 負角 負角 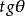 負角 負角 |
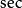 負角 負角 | 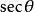 負角 負角 | 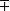 負角 負角 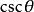 負角 負角 | 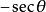 負角 負角 | 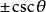 負角 負角 |
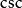 負角 負角 | 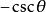 負角 負角 | 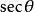 負角 負角 | 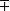 負角 負角 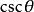 負角 負角 | 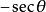 負角 負角 |