定義
B是基數為 n的集合劃分數目。集合 S的一個劃分是定義為 S的兩兩不相交的非空子集的族,它們的並是 S。例如 B = 5因為3個元素的集合{ a, b, c}有5種不同的劃分方法:
{{a}, {b}, {c}}
{{a}, {b, c}}
{{b}, {a, c}}
{{c}, {a, b}}
{{a, b, c}}
 貝爾數
貝爾數 貝爾數
貝爾數 貝爾數
貝爾數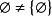 貝爾數
貝爾數B是1因為空集正好有1種劃分方法。劃分的定義要求空集的劃分中的每個成員都是非空集合,而它們的並是本身。所以是它自身的唯一划分。(這是定義所允許的因為)
公式
貝爾數適合遞推公式:
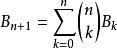 貝爾數
貝爾數它們也適合“Dobinski公式”:
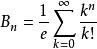 貝爾數
貝爾數期望值為1的泊松分布的''n''次矩。
它們也適合“Touchard同餘”:若p是任意質數,那么
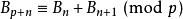 貝爾數
貝爾數每個貝爾數都是"第二類Stirling數"的和
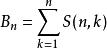 貝爾數
貝爾數Stirling數S(n, k)是把基數為n的集劃分為正好k個非空集的方法的數目。
把任一機率分布的n次矩以首n個累積量表示的多項式,其係數和正是第n個貝爾數。這種數劃分的方法不像用Stirling數那個方法粗糙。
貝爾數的指數母函式是
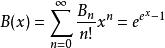 貝爾數
貝爾數貝爾三角形
用以下方法建構一個三角矩陣(形式類似楊輝三角形):
(1) 第一行第一項是1(a_{1,1} = 1)
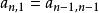 貝爾數
貝爾數(2) 對於 n>1,第n行第一項等同第n-1行最後一項。()
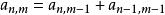 貝爾數
貝爾數(3) 對於 m, n>1,第n行第m項等於它左邊和左上方的兩個數之和。()
結果如下:(OEIS的A011971數列 )
 貝爾數
貝爾數每行首項是貝爾數。
這個三角形稱為貝爾三角形、Aitken陣列或Peirce三角形(Bell triangle, Aitken's array, Peirce triangle)。
程式
計算貝爾數的程式如下:(VC++環境下調試通過)
#include<iostream>
#include <stdio.h>
using namespace std;
unsigned __int64 c(int n,int m){
if(m>n/2)
m=n-m;
int i;
unsigned __int64 a=1,b=1;
for(i=n;i>n-m;i--)
a*=i;
for(i=2;i<=m;i++)
b*=i;
return a/b;
}
unsigned __int64 bell(int n){
unsigned __int64 t=0;
int i;
if(n==0)
return 1;
else{
for(i=0;i<=n-1;i++)
t+=c(n-1,i)*bell(i);
}
return t;
}
int main(){
int n;
while(scanf("%d",&n)!=EOF)
printf("%I64u\n",bell(n));
return 0;
}

