謝瓦萊，C.
正文
法國數學家,布爾巴基學派的創始人之一。1909年2月11日生於約翰內斯堡,1984年6月28日卒於巴黎。1926年考入巴黎高等師範學校，1929年畢業，並取得國立中學高級教師職銜，1933年獲博士學位。1931～1937年得到法國國家科學研究基金(後改中心)CNRS資助。1931～1933年赴德國學習訪問，深受（A.）E.諾特、E.阿廷等人的影響。1937年赴雷恩大學工作。1938年赴美國，先後在普林斯頓大學 (1938～1948)、哥倫比亞大學(1948～1955)任教。1953～1954年間在日本講學,對日本戰後數學復興很有影響。1955年回到法國，在巴黎大學任教，1978年退休。他在代數數論──類域論、李代數上同調理論、李群論、代數群論、有限群論、交換環論和代數幾何等方面都有重要的貢獻。 他於1936、1940年引進了伊代爾(idele)的概念,把關於有限阿貝爾擴張的阿廷映射推廣到任意阿貝爾擴域上去，並以此而對1920年高木貞治推廣希爾伯特類域論的重要工作給出了一個完全算術化的證明。後來，這個概念和與它相聯繫的阿代爾的概念也被定義於代數數域上的代數群，而且在其算術性質的研究中起了很重要的作用。
1948年謝瓦萊與S.艾倫伯格建立了李代數的上同調理論。
É.(-J.)嘉當與（C.H.）H.外爾於1890～1930年間,對於復半單李代數的構造和表示得到了深入的結果並對於李群的支撐空間的大範圍結構進行了開創性的工作。謝瓦萊於40年代系統化並完善化這些工作。他的《李群論》的專著已經成為經典著作。
1955年他證明了，對於複數域上任一單李代數L,皆可選一組基使其結構常數都是整數，從而可以構造一個相應的整數環Z上的李代數LZ。隨之對任一域F,可得F上的李代數
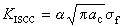由此用統一的方法可對任意有限域Fq上李代數
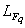均得到相應的有限群,其換位子群一般為單群，現稱為謝瓦萊群。這是對有限單群完全分類問題的一個重大貢獻。晚年他領導了一些青年數學家進行有限群表示論的研究。 複數域上的線性代數群首先為L.毛瑞爾和(C.-)É.皮卡在19世紀後半葉所研究。直到1940～1945年間，謝瓦萊用李代數方法首先將代數群推廣到其他的特徵零的域上。1956～1958年謝瓦萊完成了任意特徵的代數閉域上半單代數群的完全分類。
他與A.韋伊分別於40年代中建立起代數幾何的交點理論。他發展了由W.克魯爾創始的局部環的理想理論，引入了拓撲的概念而套用於交點理論。
