概念介紹
謝瓦萊群(Chevalley group)是與一類特殊李代數密切相關的群。設L是複數域上單李代數,Π是L的基礎根系,Φ是L的根系,
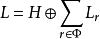 謝瓦萊群
謝瓦萊群是L的嘉當分解。根據謝瓦萊基定理,可以取嘉當子代數的基{h|α∈Π}及每個根子空間L的基e,使L關於基{h,e|α∈Π,r∈Φ}的乘法常數全是有理整數.這組基的整係數線性組合的全體L,按L的李乘法構成有理整數環Z上一個李代數.對任意域K,可將加群L=KL定義成一個李代數,使[1x,1y]=1[x,y].對任意r∈Φ與t∈K,ad(te):x→[te,x]是L的冪零微分,
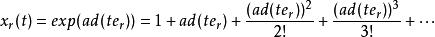 謝瓦萊群
謝瓦萊群是L的自同構。所有的x(t)(r∈Φ,t∈K)生成的群L(K)是L的自同構群的一個子群,稱為K上的謝瓦萊群。每個x(t)(t∈Φ,t∈K) 稱為L(K)的根元素,而X={x(t)|t∈K}稱為L(K)的根子群。當L分別是A(l≥1),B(l≥2),C(l≥3),D(l≥4),E(6≤l≤8),F,G型李代數時,分別得到謝瓦萊群A(K),B(K),C(K),D(K),E(K),F(K),G(K).其中A(K),B(K),C(K),D(K)分別同構於典型群PSL(K),PΩ(K,Q)(Q的指數=l),PSp(K),PΩ(K,Q)(Q的指數=l)。當K是q元有限域時,也將L(K)簡記為L(q)。除A(2),A(3),B(2),G(2)外,謝瓦萊群都是單群。
群
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。
設G為一個非空集合,a、b、c為它的任意元素。如果對G所定義的一種代數運算“·”(稱為“乘法”,運算結果稱為“乘積”)滿足:
(1)封閉性,a·b∈G;
(2)結合律,即(a·b)c = a·(b·c);
(3)對G中任意元素a、b,在G中存在惟一的元素x,y,使得a·x= b,y·a=b,則稱G對於所定義的運算“·”構成一個群。例如,所有不等於零的實數,關於通常的乘法構成一個群;時針轉動(關於模12加法),構成一個群。
滿足交換律的群,稱為交換群。
群是數學最重要的概念之一,已滲透到現代數學的所有分支及其他學科中。凡是涉及對稱,就存在群。例如,可以用研究圖形在變換群下保持不變的性質,來定義各種幾何學,即利用變換群對幾何學進行分類。可以說,不了解群,就不可能理解現代數學。
1770年,拉格朗日在討論代數方程根之間的置換時,首先引入群的概念,而它的名稱,是伽羅華在1830年首先提出的。
單群
單群是一類重要的群。即不含非平凡正規子群的群。若群G≠{e},且除{e}及G本身外不再含其他的正規子群。則稱G為單群。若此時G還是有限群,則稱G為有限單群。有限單群的例子有:素數階群,交錯群A,n≥5。有限單群的研究是有限群論中一個十分活躍的領域。
李代數
一類重要的非結合代數。非結合代數是環論的一個分支,與結合代數有著密切聯繫。結合代數的定義中把乘法結合律刪去,就是非結合代數。
李代數是挪威數學家S.李在19世紀後期研究連續變換群時引進的一個數學概念,它與李群的研究密切相關。在更早些時候,它曾以含蓄的形式出現在力學中,其先決條件是“無窮小變換”概念,這至少可追溯到微積分的發端時代。可用李代數語言表述的最早事實之一是關於哈密頓方程的積分問題。S.李是從探討具有r個參數的有限單群的結構開始的,並發現李代數的四種主要類型。法國數學家É.嘉當在1894年的論文中給出變數和參變數在複數域中的全部單李代數的一個完全分類。他和德國數學家基靈都發現,全部單李代數分成4個類型和5個例外代數,É.嘉當還構造出這些例外代數。É.嘉當和德國數學家外爾還用表示論來研究李代數,後者得到一個關鍵性的結果。“李代數”這個術語是1934年由外爾引進的。隨著時間的推移,李代數在數學以及古典力學和量子力學中的地位不斷上升。到20世紀80年代,李代數不再僅僅被理解為群論問題線性化的工具,它還是有限群理論及線性代數中許多重要問題的來源。李代數的理論不斷得到完善和發展,其理論與方法已滲透到數學和理論物理的許多領域。
一類重要的非結合代數。記L為域F上的線性空間,若L中除了加法和純量積,還有第三種代數運算:L×L→L,記為[x,y],x,y∈L,它適合條件:
1.反對稱性 [x,x]=0, x∈L.
2.雙線性性 [λx+μy,z]=λ[x,z]+μ[y,z],λ,μ∈F,x,y∈L.
3.Jacobi恆等式 [[x,y],z]+[[z,x],y]+[[y,z],x]=0,x,y,z∈L.
則[x,y]稱為x和y的換位運算,亦稱“方括弧運算”.這時L稱為域F上李代數,簡稱李代數.當L的維數有限時,稱為有限維李代數;當L的維數無限時,稱為無限維李代數。例如,若L為域F上的結合代數,滿足結合律的乘法,記為ab,a,b∈L,則運算[a,b]=ab-ba,a,b∈L為換位運算。在此運算下,L為李代數。特別地,若L為由所有n×n矩陣構成的結合代數,則在矩陣運算下定義:
[A,B]=AB-BA
便構成一個n維李代數。
單李代數
單李代數是一類結構簡單的李代數。設L為域F上的李代數,若L的非零理想只有L本身,且[L,L]≠0,則L稱為單李代數。單李代數必為半單李代數,反之,在實數及複數的情形,半單李代數必為單理想子代數的直和,因此,研究實及復半單李代數的問題化為研究實及復單李代數。
人物簡介
謝瓦萊是法國數學家。生於南非的約翰內斯堡。謝瓦萊的祖父是瑞士鐘錶匠,後定居法國。父親曾在中學教書,後進入外交界,謝瓦萊出生時他正擔任法國駐約翰內斯堡領事。謝瓦萊主要在巴黎接受教育。1926年考入巴黎高等師範學校,1929年畢業,1934年獲理科博士學位。這段期間曾到德國幾所大學訪問, 對諾特(E.Noether)、阿廷(E.Artin)以及哈瑟(H.Hasse)等人的工作留下深刻印象。回國後到雷恩大學執教。1939年應邀到美國普林斯頓高級研究所訪問。因第二次世界大戰爆發,法國被德軍占領,謝瓦萊不得不滯留美國,在普林斯頓大學任教授。1949—1955年任哥倫比亞大學教授。1955年回法國任巴黎大學教授,直至1978年退休任榮譽教授。
謝瓦萊是法國科學院院士,倫敦數學會榮譽會員。1937年在巴黎獲法蘭克爾獎,1941年獲美國數學會的柯爾獎。
謝瓦萊主要研究代數數論、代數幾何和李群,他是布爾巴基學派的最早成員之一,對現代數學發展有傑出貢獻。他在1933年的博士論文直接從p-進域出發考慮阿貝爾擴張,建立了一個局部類域論的體系,進而大大簡化了類域論中一些重要定理的證明。其後幾年,他致力於把類域論從有理數域推廣到無窮次擴張數域上去,以取消人們對Zeta函式的依賴。終於在1936年引進了伊代爾(idele)的概念,從而達到目的。1940年以後,轉向研究代數幾何和李群。他證明了代數簇局部環的一些主要性質,並創立了交截理論。他獲得“緊緻李群是代數群”這一著名定理。1955年,他發表用代數群來研究李型單群的工作,其結果與方法均有重要意義。他還致力於把基林和嘉當的關於復半單群的工作推廣到特徵為零的代數閉域和有限特徵的代數閉域上。50年代,他主持了一個代數幾何和群論討論班,在數學界甚有影響。60年代以後,他開始研究有限群論。
謝瓦萊發表了40多篇研究論文和10多部專著。其中三卷集的《李群論》(Theory ofLie Groups,1946,1951,1955)等屬數學經典著作。
