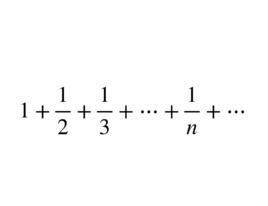簡介
調和級數是各項倒數為等差數列的級數,通常指項級數
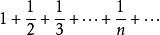 調和數列
調和數列各項倒數所成的數列(不改變次序)為等差數列。從第2項起,它的每一項是前後相鄰兩項的調和平均,故名調和級數。
推而廣之,具有這種性質的每一個級數,即形如
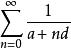 調和數列
調和數列的級數也稱為調和級數,其中 a,b 是常數. 調和級數是發散的,但其部分和
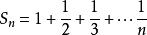 調和數列
調和數列增長極慢。
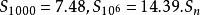 調和數列
調和數列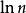 調和數列
調和數列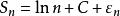 調和數列
調和數列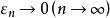 調和數列
調和數列歐拉 (Euler,L.) 計算過與是等價無窮大,更準確地,有,其中 C=0.557 215... 是歐拉常數,。這是歐拉於1740 年發現的,更一般地,級數
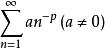 調和數列
調和數列稱為廣義調和級數,亦簡稱調和級數,它的通俗名稱是 p 級數,當 p>1 時收斂,p<=1 時發散。
定義
定義1:正整數的倒數組成的數列,稱為調和數列。
 調和數列
調和數列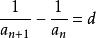 調和數列
調和數列 調和數列
調和數列定義2:若數列滿足(n∈N*,d為常數),則稱數列調和數列。
性質
調和數列的前n項和不是整數
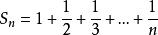 調和數列
調和數列對任意正整數n∈N,有不是整數。
 調和數列
調和數列 調和數列
調和數列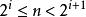 調和數列
調和數列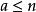 調和數列
調和數列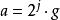 調和數列
調和數列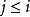 調和數列
調和數列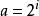 調和數列
調和數列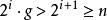 調和數列
調和數列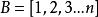 調和數列
調和數列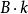 調和數列
調和數列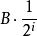 調和數列
調和數列 調和數列
調和數列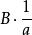 調和數列
調和數列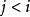 調和數列
調和數列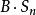 調和數列
調和數列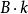 調和數列
調和數列 調和數列
調和數列證明:若不然,則令( k∈ Z)。考察正整數,使得,由整數的唯一分解性,對任意整數有,其中(事實上若且唯若時等號取得,若不然則有,矛盾!)。令為1— n最低公倍數,則有為偶數(因為 B中顯然有因子2),但為奇數(因為B中最多只有個因子2),為偶數(因為)。故有為奇數但為偶數,矛盾!所以假設不成立,非整。
調和級數發散
人們已經研究調和數列已經幾百年了.但是迄今為止沒有能得到它的求和公式只是得到它的近似公式(當n很大時):
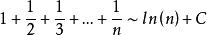 調和數列
調和數列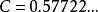 調和數列
調和數列(稱作歐拉常數,專為調和級數所用,至今不知是有理數還是無理數)
人們傾向於認為它沒有一個簡潔的求和公式。但是,不是因為它是發散的,才沒有求和公式。相反的,例如等差數列是發散的,公比的絕對值大於1的等比數列也是發散的,它們都有求和公式。
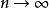 調和數列
調和數列當時
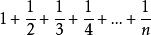 調和數列
調和數列 調和數列
調和數列這個級數是發散的。簡單的說,結果為
------------------
用高中知識也是可以證明的,如下:
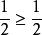 調和數列
調和數列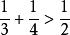 調和數列
調和數列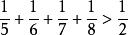 調和數列
調和數列 調和數列
調和數列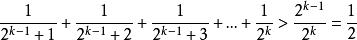 調和數列
調和數列 調和數列
調和數列 調和數列
調和數列 調和數列
調和數列 調和數列
調和數列對於任意一個正數,把分成有限個,必然能夠找到,使得
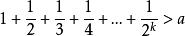 調和數列
調和數列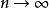 調和數列
調和數列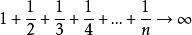 調和數列
調和數列所以時,
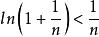 調和數列
調和數列(由也可證明)。