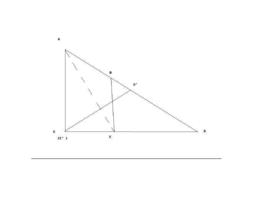
概念
由直角三角形中已知的邊和角,計算出未知的邊和角的過程,叫做解直角三角形。
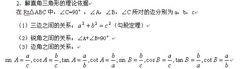 解直角三角形的理論依據
解直角三角形的理論依據特殊角值
(資料來源《數學》 )
| 銳角α | 0° | 30° | 45° | 60° | 90° |
| sin α(正弦) | 0 |  解直角三角形 解直角三角形 | 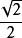 解直角三角形 解直角三角形 | 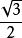 解直角三角形 解直角三角形 | 1 |
| cosα(餘弦) | 1 | 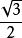 解直角三角形 解直角三角形 | 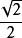 解直角三角形 解直角三角形 |  解直角三角形 解直角三角形 | 0 |
| tan α(正切) | 0 | 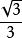 解直角三角形 解直角三角形 | 1 | 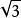 解直角三角形 解直角三角形 | 無限大 |
| cot α(餘切) | 無限大 | 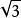 解直角三角形 解直角三角形 | 1 | 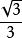 解直角三角形 解直角三角形 | 0 |
上表為部分角度,其它角度可以使用計算器計算。
銳角三角
sinA=a/c,cosA=b/c,tanA=a/b,cotA=b/a
互餘角的三角函式值之間的關係
若∠ A+∠ B=90°,那么sinA=cosB或sinB=cosA
同角的三角函式值之間的關係
①sin²A+cos²A=1
②tanA=sinA/cosA
③tanA=1/tanB
④a/sinA=b/sinB=c/sinC
銳角三角函式隨角度的變化規律
銳角∠A的tan值和sin值隨著角度的增大而增大,cos值和cot值隨著角度的增大而減小。
符號 sin cos tan cot sec csc
正弦函式sin(A)=a/c
餘弦函式cos(A)=b/c
正切函式tan(A)=a/b
餘切函式cot(A)=b/a
其中a為對邊,b為鄰邊,c為斜邊
歸納
利用解直角三角形的知識解決實際問題的一般過程:
將實際問題抽象為數學問題(畫出平面圖形,轉化為解直角三角形的問題)。
根據條件的特點,適當選用銳角三角形函式等去解直角三角形;
得到數學問題的答案。
得到實際問題的答案。
1.將實際問題抽象為數學問題(畫出平面圖形,轉化為解直角三角形的問題)。
2.根據條件的特點,適當選用銳角三角形函式等去解直角三角形;
3.得到數學問題的答案。
4.得到實際問題的答案。
 解直角三角形
解直角三角形 解直角三角形
解直角三角形