解析解的定義
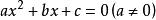 解析解
解析解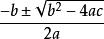 解析解
解析解所謂的 解析解是一種包含分式、三角函式、指數、對數甚至無限級數等基本函式的解的形式。用來求得 解析解的方法稱為解析法。比如一元二次方程: ,其求解公式是 ,這就是解析解。
在數學上,如果一個方程或者方程組存在至少一個由有限次常見運算給出的解,則稱該方程存在解析解。二次方程的根就是一個解析解的典型例子。在低年級數學的教學當中,解析解也被稱為公式解。
當解析解不存在時,比如五次以及更高次的代數方程,則該方程只能用數值分析的方法求解近似值。
解析解的準確含義依賴於何種運算稱為常見運算或常見函式。傳統上,只有初等函式被看作常見函式,無窮級數、序列的極限、連分數等都不被看作常見函式。按這種定義,許多累積分布函式無法寫成解析形式。但如果我們把特殊函式,比如誤差函式或伽瑪函式也看作常見函式,則累積分布函式可以寫成解析形式。
在計算機套用中,這些特殊函式因為大多有現成的數值法實現,它們通常被看作常見運算或常見函式。實際上,在計算機的計算過程中,多數基本函式都是用數值法計算的,所以所謂的基本函式和特殊函式對計算機而言並無區別。
解析解與數值解的區別
數值解(numerical solution)是採用某種計算方法,如有限元的方法,數值逼近,插值的方法,得到的解。別人只能利用數值計算的結果,而不能隨意給出自變數並求出計算值。
比如上面給出了一元二次方程的解析解,在求一個已知係數的一元二次方程時,將係數的具體取值代入則可以得到其數值解。
可以這樣來理解二者的區別,解析解是一個求解公式,它適用於所有這類方程的求解,而數值解是某個特定方程的具體的解。
例子
方程 2y=x
解:
y=0.5x——解析解
x=1時,y=0.5——數值解
