簡介
數學中， 複數平面（complex plane）是用水平的 實軸與垂直的 虛軸建立起來的複數的幾何表示。它可視為一個具有特定代數結構 笛卡兒平面（實平面），一個複數的實部用沿著 x-軸的位移表示，虛部用沿著 y-軸的位移表示。
複數平面有時也叫做 阿爾岡平面，因為它用於 阿爾岡圖中。這是以讓-羅貝爾·阿爾岡（1768-1822）命名的，儘管它們最先是挪威-丹麥土地測量員和數學家卡斯帕爾·韋塞爾（1745-1818）敘述的。阿爾岡圖經常用來標示複平面上函式的極點與零點的位置。
圖1.複數平面複平面的想法提供了一個複數的幾何解釋。在加法下，它們像向量一樣相加；兩個複數的乘法在極坐標下的表示最簡單——乘積的長度或模長是兩個絕對值或模長的乘積，乘積的角度或輻角是兩個角度或輻角的和。特別地，用一個模長為 1 的複數相乘即為一個旋轉 。
特點
建立了直角坐標系來表示複數的平面叫做複平面，x軸叫做實軸，y軸除去原點的部分叫做虛軸，原點表示實數0，原點不在虛軸上。複平面內的每一個點，有唯一的一個複數和它對應，反過來，每一個複數，有複平面內唯一的一個點和它對應，所以複數集C和複平面內所有的點所成的集合是一一對應的。
幾何表示
1.三角表示式
複數平面
複數平面
複數平面
複數平面 複數平面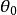
複數平面
複數平面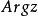 複數平面
複數平面
複數平面
複數平面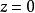 複數平面
複數平面
複數平面
複數平面
複數平面
複數平面
複數平面
複數平面 複數平面
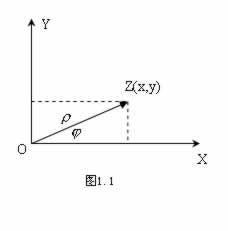
複數平面在
的情況下，以正實軸為始邊，以表示的向量為終邊的角的弧度數稱為的輻角，記作。這時有： 任意一個複數有無窮多個輻角。如果是其中的一個，那么，（為任意整數），就給出了z的全部輻角。在（）的輻角中，我們把滿足的稱為的主值，。當時，，而輻角不確定。利用直角坐標與極坐標的關係：，把表示成稱為複數的三角表示式。
2.指數表示式
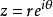複數平面
複數平面利用歐拉公式，可以得到，稱為複數的指數表達式。
數學史
17世紀時，英國數學家瓦里士已經意識到在直線上不能找到虛數的幾何表示。
1797年，挪威的測量學家維塞爾向丹麥科學院遞交論文《方向的解析表示，特別套用於平面與球面多邊形的測定》，首先提出把複數用坐標平面上的點來表示，使全體複數與平面上的點建立了一一對應關係，形成了複平面概念。但當時沒有受到人們的重視。
1806年，日內瓦的阿工在巴黎發表的論文《虛量，它的幾何解釋》，也談到了複數的幾何表示法。他用“模”這個名詞來表示向量的長度，模這術語就源出於此。
偉大的德國數學家高斯是近代數學的奠基人之一，在歷史上影響之大，可以和阿基米德、牛頓、歐拉並列。他在1799年已經知道複數的幾何表示，在1799年、1815年、1816年對代數基本定理作出的三個證明中，都假定了複數和直角坐標平面上的點一一對應，但直到1831年他才對複平面作出詳細的說明。他說：“迄至目前為止，人們對於虛數的考慮，依然在很大的程度上把虛數歸結為一個有毛病的概念，以致給虛數蒙上一層朦朧而神奇色彩。我認為只要不把+1、-1、i 叫做正一、負一和虛一，而稱之曰向前一，反向一和側向一，那么這層朦朧而神奇的色彩即可消失。”此後，人們才接受了複平面的思想，有些人還把複平面稱為高斯平面。
利用複數的幾何表示法，複數又可以用坐標平面上的向量來表示，兩個複數相加可以按照向量加法的平行四邊形法則來進行，一個複數乘以i（或-i）相當於表示此複數的向量逆（或順）時針旋轉90。這就使得物理上的許多向量：力、速度、加速度等等，都可以藉助於複數來進行計算，使複數成為物理學和其他自然科學的重要工具。
