兔子問題
13世紀義大利數學家斐波那契在他的《算盤書》中提出這樣一個問題:有人想知道一年內一對兔子可繁殖成多少對,便築了一道圍牆把一對兔子關在裡面。已知一對兔子每一個月可以生一對小兔子,而一對兔子出生後.第三個月開始生小兔子假如一年內沒有發生死亡,則一對兔子一年內能繁殖成多少對?
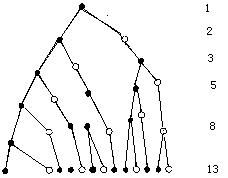
現在我們尋求兔子繁殖的規律。成熟的一對兔子用記號"紅方塊表示",未成熟的用"黑方塊"表示。"綠色線代表:延續和成長""藍色線代表:出生"。
 兔子問題
兔子問題分:可以看出六個月兔子的對數是1,1,2,3,5,8,13。很容易發現這個數列的特點:即從第三項起,每一項都等於前兩項之和。所以按這個規律寫下去,便可得出一年內兔子繁殖的對數:1,1,2,3,5,8,13,21,34,55,89,144。可見一年內兔子共有144對(第一個月和第二個月都只有1對兔子)。
還有題中本質上有兩類兔子:一類是能生殖的兔子,稱為成年兔子;新生的兔子不能生殖;新生兔子一個月就長成成年兔子。求的是成年兔子與新生兔子的總和。每月新生兔對數等於上月成年兔對數。每月成年兔對數等於上個月成年兔對數與新生兔對數之和。
法國數學家比內(Binet)證明了通項公式
為
F(1)=F(2)=1;
F(n)=F(n-1)+F(n-2) (n≥3)。
我們用機算機C語言可以對上半張圖列出以下程式:
#include "stdio.h"
#include "conio.h"
void main()
{ int i;long int f1,f2;
f1=1,f2=2;//f1代表第一個月,f2代表第二個月
for(i=1;i<=6;i++)
{
printf("%12ld%12ld",f1,f2);
f1+=f2; //斐波那契係數為第一個月加第二個月等於第三個的值
f2+=f1; //斐波那契係數為第一個月加第二個月等於第三個的值.
if(i%3==0)printf("\n");//每行列出六個數.
}
}
人們為了紀念斐波那契,就以他的名字命名這個數列為斐波那契數列,該數列的每一項稱為斐波那契數。斐波那契數列有許多有趣的性質。除了a(n)=a(n-1)+a(n-2)外,還可以證明它的通項公式為:
a(n)=(((1+5^(1/2))/2)^n-((1-5^(1/2))/2)^n)/5^(1/2)
可它的每一項卻都是整數。而且這個數列中相鄰兩項的比值,越靠後其值越接近0.618黃金比例。這個數列有廣泛的套用,如樹的年分枝數目就遵循斐波那契數列的規律;而且計算機科學的發展,為斐波那契數列提供了新的套用場所。
#include
using namespace std;
int main()
{
int i,a={0,1,1};//數組的定義,用來儲存數據
for(i=3;i<30;i++)
{
a[i]=a[i-1]+a[i-2];//Fibonacci的算術方程
}
for(i=1;i<30;i++)
{
printf("a[%d]=%d\n",i,a[i]);//輸出
}
}
public static void main(String[] args) {
long f1 = 1;
long f2 = 1;
long fn = 1;
for (int i = 3; i < 50; i++) {
fn = f1 + f2;
f2 = f1;
f1 = fn;
System.out.println(i + "," + fn);
}
}
作者簡介
比薩的李奧納多,又稱斐波那契(Leonardo Pisano ,Fibonacci, Leonardo Bigollo,1175年-1250年),義大利數學家,西方第一個研究斐波那契數,並將現代書寫數和乘數的位值表示法系統引入歐洲。