基本介紹
實驗中只有一個影響因素.或雖有多個影響因素,但在安排實驗時只考慮一個對指標影響最大的因素,其它因素儘量保持不變的實驗,即為 單因素實驗。在生產和科學實驗中,人們為了達到優質、高產、低耗的目的,需要對有關因素的最佳點進行選擇,有關這些最佳點選擇的問題被稱為 優選問題。而利用數學原理,合理地安排實驗點,減少實驗次數,從而迅速找到最佳點的一類科學方法被稱為 優選法。單因素優選法的實驗設計包括 均分法、 對分法、 黃金分割法、 分數法等 。
均分法
均分法是在實驗範圍內,根據精度要求和實際情況,均勻地安排實驗點,在每個實驗點上進行實驗並相互比較以求得最優點的方法。在對目標函式的性質沒有全面掌握的情況下,均分法是最常用的方法,可以作為了解目標函式的前期工作,同時可以確定有效的實驗範圍。均分法的優點是得到的實驗結果可靠、合理,適用於各種實驗目的,缺點是實驗次數較多,工作量較大,不經濟。
對分法
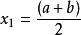 單因素實驗
單因素實驗 單因素實驗
單因素實驗 單因素實驗
單因素實驗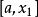 單因素實驗
單因素實驗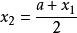 單因素實驗
單因素實驗對分法也被稱為 等分法、 平分法,也是一種簡單方便、廣泛套用的方法。對分法總是在實驗範圍[a,b]的中點 上安排實驗,根據實驗結果判斷下一步的實驗範圍,並在新範圍的中點進行實驗。如結果顯示 取大了,則去掉大於 的一半,第二次實驗範圍為 ,實驗點在其中點 上。重複以上過程,每次實驗就可以把查找的目標範圍減小一半,這樣通過7次實驗就可以將目標範圍縮小到實驗範圍的1%之內,10次實驗就可以將目標範圍縮小到實驗範圍的1‰之內。對分法的優點是每次實驗能去掉實驗範圍的50%,取點方便,實驗次數大大減少。缺點是適用範圍較窄,要根據上一次實驗結果得到下一次實驗範圍 。
黃金分割法
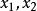 單因素實驗
單因素實驗黃金分割法也稱為 0.618法,適用於實驗指標或目標函式是單峰函式的情況,即在實驗範圍內只有一個最優點,且距最優點越遠的實驗結果越差。具體步驟是每次在實驗範圍內選取兩個對稱點做實驗,這兩個點(記為 )分別位於實驗範圍[a,b]的0.382和0.618的位置。其中:
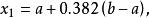 單因素實驗
單因素實驗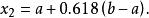 單因素實驗
單因素實驗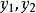 單因素實驗
單因素實驗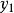 單因素實驗
單因素實驗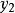 單因素實驗
單因素實驗 單因素實驗
單因素實驗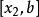 單因素實驗
單因素實驗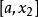 單因素實驗
單因素實驗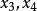 單因素實驗
單因素實驗對應的實驗結果記為 。如果 優於 ,則 是好點,把實驗範圍 划去,新的實驗範圍是 ,再重新進行黃金分割,選取兩個對稱點(記為 ),其中:
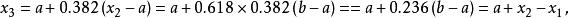 單因素實驗
單因素實驗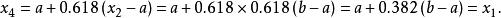 單因素實驗
單因素實驗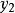 單因素實驗
單因素實驗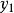 單因素實驗
單因素實驗 單因素實驗
單因素實驗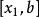 單因素實驗
單因素實驗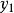 單因素實驗
單因素實驗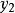 單因素實驗
單因素實驗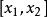 單因素實驗
單因素實驗重複以上步驟,直到找到滿意的、符合要求的實驗結果和最佳點。同理,如果 優於 ,則 是好點,新的實驗範圍是 ;如果 與 效果一樣,則去掉兩端,新的實驗范嗣是 ,之後繼續進行實驗。
用黃金分割法做實驗時,第一步需要做兩個實驗,以後每步只需要再做一個實驗,每步實驗划去實驗範圍的0.382倍,保留0.618倍。
分數法
分數法又稱為斐波納契數列法,是利用斐波納契數列進行單因素最佳化實驗設計的一種方法。斐波納契數列可由下列遞推式確定
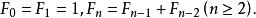 單因素實驗
單因素實驗即如下數列:
1,1,2,3,5,8,13,21,34,55,89,144,233,…
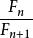 單因素實驗
單因素實驗 單因素實驗
單因素實驗 單因素實驗
單因素實驗當實驗點只能取整數,或者限制實驗次數的情況下,較難採用0. 618法進行優選,這時可採用分數法。任何小數都可以用分數表示,因此0.618也可近似地用 來表示。例如只能做4實驗,就以5/8代替0.618,第一次實驗點 在5/8處,第二個實驗點 選在其對稱點3/8處。然後通過比較實驗結果,選取新的實驗範圍進行實驗,經過重複調試便可找到滿意的結果。
分數法確定各實驗點的位置,可用下列公式求得
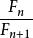 單因素實驗
單因素實驗第一個實驗點=(大數一小數)× +小數,
新實驗點=(大數-中數)+小數。
式中,中數為已實驗點數值。
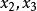 單因素實驗
單因素實驗又由於新實驗點( ,…)安排在餘下範圍內與已實驗點相對稱的點上,因此,不僅新實驗點到餘下範圍的中點的距離等於已實驗點到中點的距離,而且新實驗點到左端點的距離也等於已實驗點到右端點的距離(見圖1)即:新實驗點一左端點=右端點-已試點。
 圖1 分數法確定實驗點位置示意圖
圖1 分數法確定實驗點位置示意圖在使用分數法進行單因素優選時,應根據實驗範圍選擇合適的分數,所選擇的分數不同,實驗次數和精度也不一樣,如表1所示。
| 實驗次數 | 2 | 3 | 4 | 5 | 6 | 7 |  單因素實驗 單因素實驗 | n | |
| 等分實驗範圍的份數 | 3 | 5 | 8 | 13 | 21 | 34 |  單因素實驗 單因素實驗 | 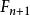 單因素實驗 單因素實驗 | |
| 第一次實驗點的位置 | 2/3 | 3/5 | 5/8 | 8/13 | 13/21 | 21/34 |  單因素實驗 單因素實驗 | 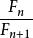 單因素實驗 單因素實驗 | |
| 精度 | 1/3 | 1/5 | 1/8 | 1/13 | 1/21 | 1/34 |  單因素實驗 單因素實驗 | 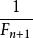 單因素實驗 單因素實驗 | |
分批實驗法
在生產和科學實驗中,為了縮短整體實驗周期,常常採用一批同時做幾個實驗的方法,即分批實驗法。分批實驗法可分為 均分分批實驗法和 比例分割分批實驗法。
均分分批實驗法
 單因素實驗
單因素實驗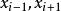 單因素實驗
單因素實驗均分分批實驗法指每批實驗均勻地安排在實驗範圍內,其示意圖如圖2所示。每批做2n個實驗,將實驗範圍均勻地分為2n+1等份,在其2n個分點處做第一批實驗。然後同時比較2n個實驗結果,留下較好的點,及其左右相鄰的兩段,即[]作為新實驗範圍。第二批實驗把這兩段都各等分為n+1段,在得到的共2n個分點處做實驗,直至得到滿意的結果。該方法適用於測定某種有毒物質進入生化處理構築物的最大允許濃度 。
 圖2 均分分批實驗法示意圖(n=2)
圖2 均分分批實驗法示意圖(n=2)比例分割分批實驗法
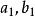 單因素實驗
單因素實驗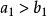 單因素實驗
單因素實驗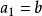 單因素實驗
單因素實驗 單因素實驗
單因素實驗比例分割分批實驗法指將實驗點按一定比例安排在實驗範圍內,其示意圖如圖3所示。每批做2n+1個實驗,把實驗範圍劃分為2n+2段,相鄰兩段長度為a和b(a>b)。在2n+1個分點上做第一批實驗,比較結果,在好實驗點左右分別留下一個a區和b區。然後把a區分成2n+2段,相鄰兩段為(),且。設短、長段的比例為,則
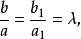 單因素實驗
單因素實驗可推知
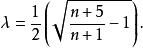 單因素實驗
單因素實驗 單因素實驗
單因素實驗 單因素實驗
單因素實驗 單因素實驗
單因素實驗由上式可知,每批實驗次數不同時,短、長段的比例是不同的。當n=2時,每批做5個實驗,=0.264。當n=0時,每批做1個實驗,=0.618。因此可認為比例分割法是黃金分割法的推廣 。
 圖3(a) 比例分割分批實驗法示意圖
圖3(a) 比例分割分批實驗法示意圖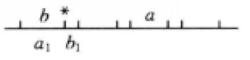 圖3(b) 比例分割分批實驗法示意圖
圖3(b) 比例分割分批實驗法示意圖
