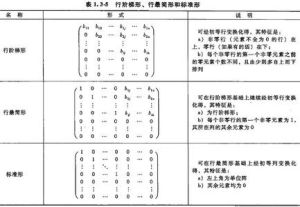
階梯形矩陣
如果:
所有非零行(矩陣的行至少有一個非零元素)在所有全零行的上面。即全零行都在矩陣的底部。
非零行的首項係數(leading coefficient),也稱作主元, 即最左邊的首個非零元素(某些地方要求首項係數必須為1),嚴格地比上面行的首項係數更靠右。
首項係數所在列,在該首項係數下面的元素都是零 (前兩條的推論).
這個矩陣是行階梯形矩陣:
化簡後的行階梯形矩陣(row echelon form), 也稱作 行最簡形矩陣(reduced row echelon form),如果滿足額外的條件:
每個首項係數是1,且是其所在列的唯一的非零元素。例如:
注意,這並不意味著化簡後的行階梯形矩陣的左部總是單位陣.
矩陣變換
通過有限步的行初等變換, 任何矩陣可以變換為行階梯形。由於行初等變換保持了矩陣的行空間, 因此行階梯形矩陣的行空間與變換前的原矩陣的行空間相同。
行階梯形的結果並不是唯一的。例如,行階梯形乘以一個標量係數仍然是行階梯形。但是,可以證明一個矩陣的化簡後的行階梯形是唯一的。
一個線性方程組是 行階梯形,如果其增廣矩陣是行階梯形. 類似的,一個線性方程組是 簡化後的行階梯形或' 規範形',如果其增廣矩陣是化簡後的行階梯形.