性質
•行最簡形矩陣是由方程組唯一確定的,行階梯形矩陣的行數也是由方程組唯一確定的。
•行最簡形矩陣再經過初等列變換,可化成標準形。
•行階梯形矩陣且稱為行最簡形矩陣,即非零行的第一個非零元為1,且這些非零元所在的列的其他元素都是零。
 行最簡形矩陣
行最簡形矩陣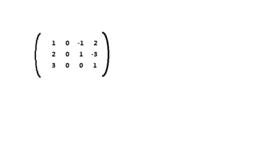
在矩陣中可畫出一條階梯線,線的下方全為0,每個台階只有一行,台階數即是非零行的行數,階梯線的豎線(每段豎線的長度為一行)後面的第一個元素為非零元,也就是非零行的第一個非零元,則稱該矩陣為行階梯矩陣。若非零行的第一個非零元都為1,且這個非零元所在的列的其他元素都為0,則稱該矩陣為行最簡形矩陣。
性質
•行最簡形矩陣是由方程組唯一確定的,行階梯形矩陣的行數也是由方程組唯一確定的。
•行最簡形矩陣再經過初等列變換,可化成標準形。
•行階梯形矩陣且稱為行最簡形矩陣,即非零行的第一個非零元為1,且這些非零元所在的列的其他元素都是零。
 行最簡形矩陣
行最簡形矩陣最簡行階梯矩陣,是一種特殊的行階梯矩陣,其各行的第1個非零元素均為1,且所在列的其他元素都為0 。
簡介 定義 示例在數學中,矩陣(Matrix)是一個按照長方陣列排列的複數或實數集合 ,最早來自於方程組的係數及常數所構成的方陣。這一概念由19世紀英國數學家凱利首先提...
歷史 定義 基本運算 乘法 行列式行階梯形矩陣,Row-Echelon Form,是指線性代數中的矩陣。
階梯形矩陣 矩陣變換如果AA=E(E為單位矩陣,A表示“矩陣A的轉置矩陣”)或AA=E,則n階實矩陣A稱為正交矩陣 。正交矩陣是實數特殊化的酉矩陣,因此總是屬於正規矩陣。盡...
定義 定理 舉例 基本構造 基本特性若矩陣A滿足兩條件:(1)若有零行(元素全為0的行),則零行應在最下方;(2)非零首元(即非零行的第一個不為零的元素)的列標號隨行標號的增加而嚴格遞增,...
階梯形矩陣 行簡化階梯形矩陣 行最簡形矩陣一看...如果要評選物理學發展史上最偉大的那些年代,那么有兩個...相對論和量子論,並最徹底地推翻和重建了整個物理學體系。所不同的是,今天當我們...的發展史是物理學上最激動人心的篇章之一,我們會看到物理大廈在狂風暴雨下轟然...
《上帝擲骰子嗎》 序 第一章 黃金時代 第二章 烏雲 第三章 火流星向量組的秩的概念 803.4.2 矩陣的行秩與列秩 823.5 向量空間...6章二次型6.1二次型及其標準形6.1.1二次型及其矩陣表 ...清大出版目錄1.行列式2.矩陣3.線性方程組4.向量空間與線性變換5....
清大出版 07年出版 05年出版 13年出版 14年出版求行階梯矩陣及向量組的基 2.7 稀疏矩陣技術 2.7.1...操作基礎、矩陣及其基本運算、與數值計算相關的基本函式、符號運算的函式... 1.5.3 演示系統 1.5.4 遠程幫助系統 第2章 矩陣及其基本運算 2.1...
內容簡介 目錄 前言相關性 2.6.2 求行階梯矩陣及向量組的基 2.7 稀疏矩陣技術...介紹了MATLAB的函式,主要包括MATLAB操作基礎、矩陣及其基本運算...:MATLAB操作基礎,矩陣及其基本運算函式,數值計算函式,符號運算函式...
基本信息 內容簡介 編輯推薦 圖書目錄