定義
若f(x)為一函式,定義域和值域都是實數,若針對每一個x,都存在ε>0 ,使得針對每一個δ>0,都可以找到y,使下式成立,則f(x)為處處不連續函式:0< |x−y|<δ 且|f(x)−f(y)|≥ε,換句話說,不論距固定點多近,都有距固定點更近的點使函式的值偏離固定點對應的值。例如狄利克雷函式就是一個處處不連續函式。
若將定義中的絕對值改為度量空間中的距離或是拓撲空間中的類似名詞。即可定義更泛用的處處不連續函式。
狄利克雷函式
簡介
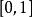 處處不連續函式
處處不連續函式狄利克雷函式(英語:Dirichlet function)是一個定義在實數範圍上、值域為的函式,是處處不連續函式。
 處處不連續函式
處處不連續函式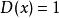 處處不連續函式
處處不連續函式當自變數 為有理數時, ;
 處處不連續函式
處處不連續函式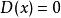 處處不連續函式
處處不連續函式當自變數 為無理數時, 。
狄利克雷函式的圖像關於y軸成軸對稱,是一個偶函式;它處處不連續;處處極限不存在;不可積分。這是一個處處不連續的可測函式。
狄利克雷函式也可以表達為一個連續函式序列的雙重點極限,如下:
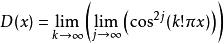 處處不連續函式
處處不連續函式 處處不連續函式
處處不連續函式 處處不連續函式
處處不連續函式,其中 和 為整數。
性質
定義在整個數軸上。
無法畫出圖像。
以任何正有理數為其周期(從而無最小正周期)。
處處無極限、不連續、不可導。
在任何區間上不黎曼可積。
是偶函式。
它在[0,1]上勒貝格可積。
1.定義在整個數軸上。
2.無法畫出圖像。
3.以任何正有理數為其周期(從而無最小正周期)。
4.處處無極限、不連續、不可導。
5.在任何區間上不黎曼可積。
6.是偶函式。
7.它在[0,1]上勒貝格可積。
超實數特性
一實數函式f為處處不連續,若其超實數延伸有以下的特性:每一個無限接近一個x都有一個無限接近的點y,使得距離f(x)-f(y)不是無窮小量。
相關條目
•Thomae函式:在無理數下連續,但在有理數下不連續的函式。
•魏爾斯特拉斯函式:一個處處連續但處處不可導的的函式。
