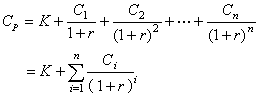薄板理論的內容
根據有關變形假設,建立板彎曲後中面的撓度微分方程,並利用邊界條件求解,得出板中面的彎曲面,進而算出板的內力分量,如彎矩、扭矩、剪力,等等。
微分方程
薄板理論是一個近似理論。薄板撓度微分方程是以下面三個假設為基礎的:①原垂直於板中面的線段仍垂直於變形後的中面;垂直於中面的正應力(見應力)遠小於平行於中面的應力分量,故可以忽略;③在垂直於板中面的載荷作用下發生彎曲時,板中面不受拉伸。其中①和③稱為基爾霍夫假設。根據這些假設導出的微分方程適用於小撓度情況,即撓度和板厚度相比為一小量。
在垂直於板中面的分布載荷作用下(圖1),薄板撓度的微分方程為:
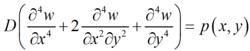 薄板理論
薄板理論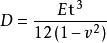 薄板理論
薄板理論式中p(x,y)為垂直於板面的分布載荷;w為載荷作用下板中面各點沿z方向的位移(即撓度);
為板的彎曲剛度,E為板材料的彈性模量,v為泊松比(見材料的力學性能);t為板厚。
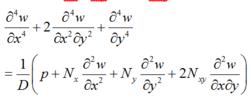 薄板理論
薄板理論如果在板的中面內還有張力N、N和剪力N(圖2),則微分方程為:
如果薄板被彈性地基支承,根據溫克勒假設,即地基的反作用力和沉陷深度成正比,則有:
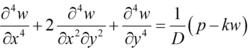 薄板理論
薄板理論式中k為地基的彈性模量。
對於正交各向異性板,彎曲面的微分方程為:
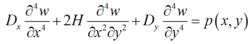 薄板理論
薄板理論式中的D、H、D均為正交各向異性板的有關常數。
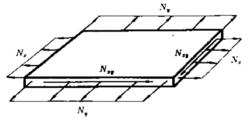 圖2 板中的內力
圖2 板中的內力上述方程通過坐標變換還可寫成其他形式,以便求解其他形狀的板。例如通過極坐標變換,可得到求解各向同性圓板彎曲面的微分方程如下:
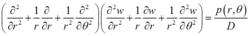 薄板理論
薄板理論邊界條件
對不同的邊界情況,邊界條件有所不同:
①固定邊沿邊緣各點的撓度和斜度均為零。在直角坐標系中,若x=a為固定邊,則
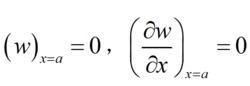 薄板理論
薄板理論②簡支邊(註:此處空格)沿簡支邊各點的撓度和彎矩M均為零。若x=a為簡支邊,則
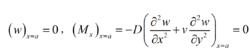 薄板理論
薄板理論③自由邊(註:此處空格)沿自由邊各點的彎矩和剪力V為零。若x=a為自由邊,則
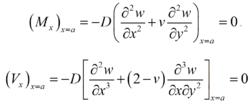 薄板理論
薄板理論④自由角點(註:此處空格)若x=a,y=b是一個自由角點,則角點的反力R為零,即
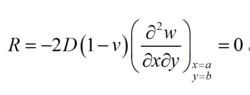 薄板理論
薄板理論求解
有兩種途徑,一是求出既滿足微分方程又滿足邊界條件的精確解(如萊維法,納維法);二是當得不到精確解時,採用各種近似方法求解,例如有限元法、有限差分方法等數值方法和能量方法。出於工程實際的需要,人們對矩形板和圓板的研究較多。