釋義
萬有引力常數提出人牛頓如果改其中G為一個常數，叫做引力常量。應該說明的是，牛頓得出這個規律，是在與胡克等人的探討中得到的。牛頓發現了萬有引力定律，但引力常量G這個數值是多少，連他本人也不知道。按說只要測出兩個物體的質量，測出兩個物體間的距離，再測出物體間的引力，代入萬有引力定律，就可以測出這個常量。但因為一般物體的質量太小了，它們間的引力無法測出，而天體的質量太大了，又無法測出質量。所以，萬有引力定律發現了100多年，萬有引力常量仍沒有一個準確的結果，這個公式就仍然不能是一個完善的等式。直到100多年後，英國人卡文迪許利用扭秤，才巧妙地測出了這個常量。
定義
萬有引力常數又稱重力常數，即萬有引力定律中表示引力與兩物體質量、距離關係公式中的係數。萬有引力常量是自然界中少數幾個最重要的物理常量之一。
其值約等於6.67259×10^(-11)N·m^2/(kg^2)；
它是在牛頓發現萬有引力定律一百多年以後，由英國物理學家卡文迪許於1798年巧妙的在實驗室里用扭秤測定的萬有引力常數，從而算出地球的質量和密度。
測量歷史
萬有引力常數最早出現在牛頓的萬有引力方程中，但是其數值直到牛頓死後的71年（1798年）才被卡文迪許(HenryCavendish)通過實驗測得。卡文迪許最初的目的不是為了測量這個常數，而是為了測量地球的質量，所以這個實驗又稱為稱地球實驗。卡文迪許得到的數值為 。之後的很長時間，這個常數的精度僅有少量的改善。常數G非常難以測量，因為引力相比試驗中的其他力來說非常微弱，而且實驗中很難避免其他物體引力的影響。而且，萬有引力常數也無法通過其他精確測量的參數間接的計算得到。歷史上發表的萬有引力常數數值變化很大。2014年，CODATA得到了精度最高的測量值。
公式
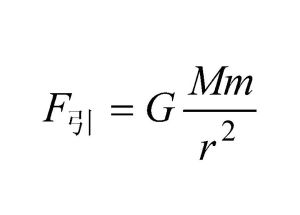萬有引力公式兩質點間的吸引力(F)與二者的質量(M和m)的乘積成正比，而與他們之間的距離(r)的平方成反比，其中的比例常數G即是萬有引力常數
適用條件：
1.只適用於計算質點間的相互作用力，即當兩個物體間的距離遠大於物體的大小時才近似適用;
2.當兩個物體距離不太遠的時候，不能看成質點時，可以採用先分割，再求矢量和的方法計算;
3.一個質量分布均勻的球體與球外一個質點的萬有引力（或兩個均勻球體間的引力），可用公式計算，這時r是指球心間距離。
實驗
卡文迪許實驗
這是一個卡文迪許扭秤的模型扭秤的主要部分是這樣一個T字形輕而結實的框架，把這個T形架倒掛在一根石英絲下。若在T形架的兩端施加兩個大小相等、方向相反的力，石英絲就會扭轉一個角度。力越大，扭轉的角度也越大。反過來，如果測出T形架轉過的角度，也就可以測出T形架兩端所受力的大小。在T形架的兩端各固定一個小球，再在每個小球的附近各放一個大球，大小兩個球間的距離是可以較容易測定的。根據萬有引力定律，大球會對小球產生引力，T形架會隨之扭轉，只要測出其扭轉的角度，就可以測出引力的大小。當然由於引力很小，這個扭轉的角度會很小。
怎樣才能把這個角度測出來呢？卡文迪許在T形架上裝了一面小鏡子，用一束光射向鏡子，經鏡子反射後的光射向遠處的刻度尺，當鏡子與T形架一起發生一個很小的轉動時，刻度尺上的光斑會發生較大的移動。這樣，就起到一個化小為大的效果，通過測定光斑的移動，測定了T形架在放置大球前後扭轉的角度，從而測定了此時大球對小球的引力。卡文迪許用此扭秤驗證了牛頓萬有引力定律，並測定出引力常量G的數值。這個數值與近代用更加科學的方法測定的數值是非常接近的。
