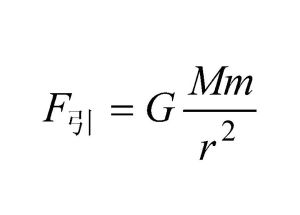概述
萬有引力=F=GmM/r^2;兩個通常物體之間的萬有引力極其微小,我們察覺不到它,可以不予考慮。比如,兩個質量都是60千克的人,相距0.5米,他們之間的萬有引力還不足百萬分之一牛頓,而一隻螞蟻拖動細草梗的力竟是這個引力的1000倍。但是,天體系統中,由於天體的質量很大,萬有引力就起著決定性的作用。在天體中質量還算很小的地球,對其他的物體的萬有引力已經具有巨大的影響,它把人類、大氣和所有地面物體束縛在地球上,它使月球和人造地球衛星繞地球鏇轉而不離去。當在某星球表面作圓周運動時,可將萬有引力看作重力,既有mg=GmM/(r²),此時有GM=gr²,為黃金代換公式。且有GmM/r²=mv²/r=mrω²=4π²mr/T²=mg。
公式
 萬有引力公式
萬有引力公式萬有引力的推導:若將行星的軌道近似的看成圓形,從克卜勒第二定律可得行星運動的角速度是一定的,即:ω=2π/T(周期)
如果行星的質量是m,離太陽的距離是r,周期是T,那么由運動方程式可得,行星受到的力的作用大小為
mrω²=mr(4π²)/T²
另外,由克卜勒第三定律可得
r三次方/T²;=常數k′
那么沿太陽方向的力為
mr(4π²)/T&²;=mk′(4π²;)/r²;
由作用力和反作用力的關係可知,太陽也受到以上相同大小的力。設太陽的質量為M,從太陽的角度看,
M(k″)(4π²)/r²
是太陽受到沿行星方向的力。因為是相同大小的力,由這兩個式子比較可知,k′包含了太陽的質量M,k″包含了行星的質量m。由此可知,這兩個力與兩個天體質量的乘積成正比,與兩個天體距離的平方成反比。