若爾當矩陣

定義

若爾當矩陣(Jordan matrix)一種重要的具有特殊形式的矩陣。

即形式為J（λ，t）

若爾當矩陣

的矩陣稱為一個若爾當塊，其中λ是複數，由若干個若爾當塊組成的準對角矩陣A

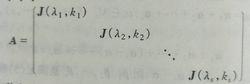若爾當矩陣

稱為一個若爾當形矩陣，其中λ，λ，… ，λ為複數有一些可以相同。

例題

如圖所示例題

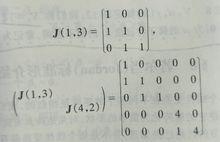若爾當矩陣

性質

設Α是複數域上n維線性空間V的一個線性變換，則V中一定存在一組基，A在這組基下的矩陣是若爾當形矩陣，並且這個若爾當形矩陣除去其中的若爾當塊的排列順序外，由A唯一決定，它稱為A的矩陣的若爾當標準形。

推論

每個n級復矩陣A一定與一個若爾當形矩陣相似，這個若爾當形矩陣除去其中若爾當塊的排列順序外由A唯一決定稱為A的若爾當標準形。