基本概念
同構
兩個數學系統(例如兩個代數系統),當它們的元素及各自所定義的運算一一對應,並且運算結果也保持一一對應,則稱這兩個系統同構,記為≌。它們對於所定義的運算,具有相同的結構。例如,十進制數與二進制數是同構的。
建立同構關係的映射,稱為同構映射。例如,當映射為一一映射,並且對應元素關於運算保持對應時,就是同構映射。
同構是數學中最重要的概念之一。在很多情況,一個難題往往可以化成另一個同構的、似乎與它不相關的、已經解決的問題,從而使原問題方便地得到解決。雖然數學發展得越來越複雜,但利用同構概念,不僅使數學得到簡化,而且使數學變得越來越統一。表面上似乎不同,但本質上等價的結果,可以用統一的形式表達出來。例如,如果四色定理得到了證明,其他數學分支中與它同構的幾十個假設,也同時得到了證明。
同態
 自同態
自同態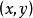 自同態
自同態 自同態
自同態 自同態
自同態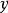 自同態
自同態 自同態
自同態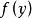 自同態
自同態 自同態
自同態設E與F為兩個群胚,它們的合成法則分別記為⊥與⊤, 稱從E到F中的映射 是群胚同態,如果對於E的任一元素偶 有 ( ⊥ )= ⊤ ,設E與F為兩個么半群(兩個群),稱從E到F中的映射, 是么半群(群)的同態,如果f是群胚的同態,且E的中性元素的象是F的中性元素, (在群的情況下,後一個條件是自然滿足的,但是從加法么半群N到乘法么半群N的映射x↦0是群胚的同態, 而並不因此就是么半群的同態)。
 自同態
自同態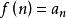 自同態
自同態 自同態
自同態 自同態
自同態 自同態
自同態 自同態
自同態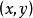 自同態
自同態設G為乘法群,而
為G的元素,由關係所定義的從加法群Z到G中的映射是群的同態。設A與B為兩個環(兩個體),稱從A到B中的映射是環(體)的同態,如果是加法群的同態,且為乘法么半群的同態, 這就是說,對A的任一元素偶,有
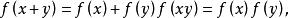 自同態
自同態並且將A的單位元變成B的單位元。
 自同態
自同態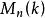 自同態
自同態例如,設n為非零自然數,使任一有理整數對應其對模n的剩餘類映射是從環Z到環Z/nZ上的同態,設E與F為兩個A-代數(兩個酉A-代數),稱從E到F中的映射 是A-代數(酉A-代數)的同態,如果它是線性映射,並且是乘法群胚(乘法么半群)的同態.。例如,設E為交換體K上的非零有限n維向量空間,而B為E的基,則從E的全體自同態之酉代數ℒ(E)到K中元素構成的全體n階方陣之酉代數 中的映射,如果該映射使E的任一自同態對應它在基B中的矩陣,則這一映射是酉代數的同態。
自同態的定義
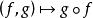 自同態
自同態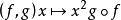 自同態
自同態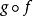 自同態
自同態自同態是已知集合(群、環、代數)到其自身保持代數結構的映射,例如線性空間到某半空間的射影就是線性空間的自同態,它保持了向量的加法運算和數乘運算。 設G為關於加法的交換群,賦以加法及法則 的G的全體自同態之集是一個環; 設E為交換體K上的向量空間,賦以法則 , E的全體自同態之向量空間是酉代數,記為ℒ(E),或End(E),元素 仍記為gf,A-模的情形是類似的。
群的自同態
 自同態
自同態 自同態
自同態設 是G到G本身的一個同態(或同構),則稱 是G上的一個自同態(endomorphism)(或自同構(automorphism)),G上的所有自同態的集合對變換的複合構成—-個含么半群,稱為G上的自同態半群(endomorphism semigroup),記作EndG,G上的所有白同構的集合對變換的複合構成一個群,稱為G上的自同構群(automorphism group),記作AutG。
 自同態
自同態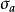 自同態
自同態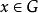 自同態
自同態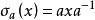 自同態
自同態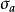 自同態
自同態在群G中,取定一個元素 ,定義G上的一個變換 為:對任何 有 ,則 是G上的一個自同構,這個自同構稱為一個內自同構(inner autmorphism),G上的全體內自同構構成一個群,稱為內自同構群(inner automorphism group),記作InnG,即
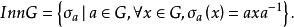 自同態
自同態內自同構群有以下性質。
定理設G是群,則
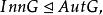 自同態
自同態(1)
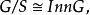 自同態
自同態(2)
其中C為G的中心。
下面通過一些例子來說明如何確定一個群的自同態半群或自同構群。
例1 設Z是整數加群,試確定AutZ。
 自同態
自同態 自同態
自同態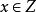 自同態
自同態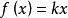 自同態
自同態 自同態
自同態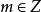 自同態
自同態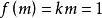 自同態
自同態解: 設 是Z的任一自同構,並設 (1)=k,則對任意 有 ,因為 是滿射,故存在 ,使 ,由此得k=1或k=-1,也就是說,只有以下兩個映射才有可能是同構映射:
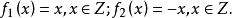 自同態
自同態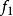 自同態
自同態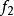 自同態
自同態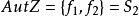 自同態
自同態不難驗證 與 確是Z上的同構,所以 。
 自同態
自同態 自同態
自同態 自同態
自同態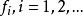 自同態
自同態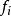 自同態
自同態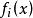 自同態
自同態通過這個簡單的例子可以說明如何確定一個群G的全部自同構(或自同態),首先分析任意一個自同構(或自同態) 的性質,主要是分析G的生成元在 下的像,從而決定 所具有的約束條件,根據這個約束條件寫出全部自同構(或自同態)。在表達方法上,最後得到的不同的自同構(或自同態)套用不同的映射記號(例如 )表示,對每一個映射 給出 的一般表達式。
環的自同態
 自同態
自同態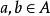 自同態
自同態設A和A’是兩個環,若有一個A到A‘’的映射 滿足以下條件:對任何 有
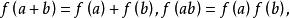 自同態
自同態 自同態
自同態則稱 是一個A到A'的同態。我們把上式稱為保持環中的運算。
 自同態
自同態 自同態
自同態如果 是單射,則稱 是一個單同態;
 自同態
自同態 自同態
自同態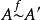 自同態
自同態如果 是滿射,則稱 是一個滿同態.這時,記作 ;
 自同態
自同態 自同態
自同態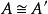 自同態
自同態如果 是雙射,則稱 是A到A'的一個同構.這時記作 。
 自同態
自同態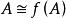 自同態
自同態 自同態
自同態當 是單同態時, ,稱 將A同構嵌入到A'中。
一個A到A本身的同態,稱為A上的 自同態,一個A到A本身的同構,稱為A上的 自同構。環A上的全體自同構關於映射的複合構成群,稱為環A上的 自同構群,記作AutA。
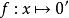 自同態
自同態 自同態
自同態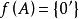 自同態
自同態例2 設A,A'是兩個環,定義映射 ,對任何x∈A,則 是A到A'的一個同態,且同態像為 ,此同態稱為零同態,是任何兩個環之間都存在的一個同態。