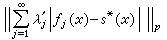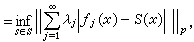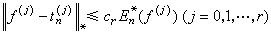聯合逼近
正文
一般是指兩個方面的逼近,其一是同時逼近函式及函式的導數,其二是用一個函式同時逼近幾個函式或者一列函式。同時逼近函式及其導數是指用一個函式逼近另一給定函式的同時,也要求其導數實現對所給函式之導數的逼近。這樣的逼近是可能的。假設函式ƒ(x)是周期為2π的連續函式,如果它有r階連續導數,則有不超過n階的三角多項式tn(x)使得
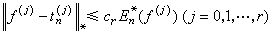 ,
,
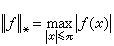 ,сr是僅與r有關的正數,E奱(ƒ)表示不超過n階的三角多項式對ƒ的最佳逼近值。假設ƒ(x)是【-1,1】上有r階連續導數的函式,則有n次代數多項式Pn(x)使得
,сr是僅與r有關的正數,E奱(ƒ)表示不超過n階的三角多項式對ƒ的最佳逼近值。假設ƒ(x)是【-1,1】上有r階連續導數的函式,則有n次代數多項式Pn(x)使得 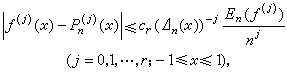
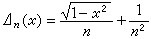 ,En(ƒ
,En(ƒ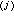 )表示不超過n次的代數多項式對ƒ
)表示不超過n次的代數多項式對ƒ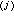 的最佳逼近值。
的最佳逼近值。 用一個函式同時逼近 n個或一列函式,有種種提法。對於【-1,1】上的可測函式ƒ(x),記使得
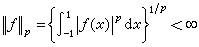
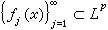 和一列非負實數
和一列非負實數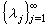 ,S為lp的一個給定的子集,如果
,S為lp的一個給定的子集,如果 
①
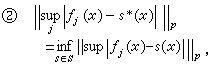 ③
③ 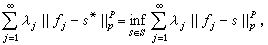
④