理論描述
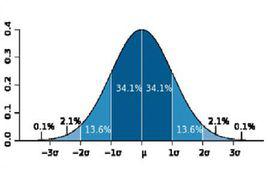
置信區間是一種常用的區間估計方法,所謂置信區間就是分別以統計量的置信上限和置信下限為上下界構成的區間 。對於一組給定的 樣本數據,其平均值為μ,標準偏差為σ,則其 整體數據的平均值的100(1-α)%置信區間為(μ-Ζσ , μ+Ζσ) ,其中α為非置信水平在常態分配內的覆蓋面積 ,Ζ即為對應的標準分數。
 置信區間
置信區間 置信區間
置信區間 置信區間
置信區間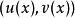 置信區間
置信區間對於一組給定的數據,定義 為觀測對象,W為所有可能的觀測結果, X為實際上的觀測值,那么 X實際上是一個定義在 上,值域在W 上的隨機變數。這時,置信區間的定義是一對函式 u(.) 以及 v(.) ,也就是說,對於某個觀測值 X= ,其置信區間為 。實際上,若真實值為 w,那么置信水平就是機率 c:
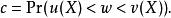 置信區間
置信區間其中U=u(X)和 V=v(X)都是統計量(即可觀測的隨機變數),而置信區間因此也是一個隨機區間:(U,V) 。
計算公式
置信區間的計算公式取決於所用到的統計量。置信區間是在預先確定好的顯著性水平下計算出來的,顯著性水平通常稱為α(希臘字母alpha),如前所述,絕大多數情況會將α設為0.05。置信度為(1-α),或者100×(1-α)%。於是,如果α=0.05,那么置信度則是0.95或95%,後一種表示方式更為常用 。置信區間的常用計算方法如下:
Pr(c1<=μ<=c2)=1-α
其中:α是顯著性水平(例:0.05或0.10);
Pr表示機率,是單詞probablity的縮寫;
100%*(1-α)或(1-α)或指置信水平(例如:95%或0.95);
表達方式:interval(c1,c2) - 置信區間。
求解步驟
第一步:求一個樣本的均值
第二步:計算出抽樣誤差。經過實踐,通常認為調查:100個樣本的抽樣誤差為±10%;500個樣本的抽樣誤差為±5%;1200個樣本時的抽樣誤差為±3%。
第三步:用第一步求出的“樣本均值”加、減第二步計算的“抽樣誤差”,得出置信區間的兩個端點 。
主要性質
較窄的置信區間比較寬的置信區間能提供更多的有關總體參數的信息 。舉例說明如下:
假設全班考試的平均分數為65分,則有如下表格中的理解:
| 置信區間 | 間隔 | 寬窄度 | 表達的意思 |
| 0-100分 | 100 | 寬 | 等於什麼也沒告訴你 |
| 30-80分 | 50 | 較窄 | 你能估出大概的平均分了(55分) |
| 60-70分 | 10 | 窄 | 你幾乎能判定全班的平均分了(65分) |
相關聯繫
置信區間與置信水平、樣本量等因素均有關係,其中樣本量對置信區間的影響為:在置信水平固定的情況下,樣本量越多,置信區間越窄。其次,在樣本量相同的情況下,置信水平越高,置信區間越寬。實例分析如下:
(1)置信區間與樣本量關係分析
| 樣本量 | 置信區間 | 間隔 | 寬窄度 |
| 100 | 50%-70% | 20 | 寬 |
| 800 | 56.2%-63.2% | 7 | 較窄 |
| 1,600 | 57.5%-63% | 5.5 | 較窄 |
| 3,200 | 58.5%-62% | 3.5 | 更窄 |
由上表得出:
1、在置信水平相同的情況下,樣本量越多,置信區間越窄。
2、置信區間變窄的速度不像樣本量增加的速度那么快,也就是說並不是樣本量增加一倍,置信區間也變窄一半(實踐證明,樣本量要增加4倍,置信區間才能變窄一半),所以當樣本量達到一個量時(通常是1,200),就不再增加樣本了。故:置信區間=點估計 ±(關鍵值 × 點估計的標準差)。在其他因素不變的情況下,樣本量越多(大),置信區間越窄(小)。
(2)置信區間與置信水平關係分析
美國做了一項對總統工作滿意度的調查。在調查抽取的1,200人中,有60%的人讚揚了總統的工作,抽樣誤差為±3%,置信水平為95%;如果將抽樣誤差減少為±2.3%,置信水平降到為90%。則兩組數字的情況比較如下:
| 抽樣誤差 | 置信水平 | 置信區間 | 間隔 | 寬窄度 |
| ±3% | 95% | 60%±3%=57%-63% | 6 | 寬 |
| ±2.3% | 90% | 60%±2.3%=57.7%-62.3% | 4.6 | 窄 |
由上表得出:
在樣本量相同的情況下(都是1,200人),置信水平越高(95%),置信區間越寬 。