基本介紹
置信界限又稱置信限,是對單側置信區間中的界限以及雙側置信區間的上、下限的統稱。置信區間是用一種特定的可能性(置信程度或置信倒數)能說明的一個範圍(區間),它有一個要求去測定的參數,這個參數可能是平均數、標準誤差、一種比例數或任何其他測定點,目的是確定較高和較低的置信界限。
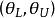 置信界限
置信界限對於總體參數 θ進行區間估計時,如果預先給定一個很小的機率α,就能找到 一個區間,使得:
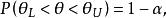 置信界限
置信界限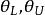 置信界限
置信界限那么,就稱為 置信界限。
區間估計
在實際問題中往往需要由 樣本估計出未知參數的一個範圍,並且能指出有多大把握預言未知參數不超過這個範圍,這個範圍通常以區間形式給出,就是用區間作為未知參數的估計,並且說明這個區間包含參數真值的機率,這樣的區間稱為 置信區間,這種估計稱為參數的 區間估計。
 置信界限
置信界限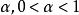 置信界限
置信界限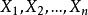 置信界限
置信界限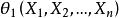 置信界限
置信界限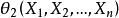 置信界限
置信界限定義 設總體X的分布中含有未知參數,對於給定值,若由樣本確定的兩個統計量和滿足
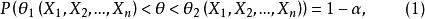 置信界限
置信界限 置信界限
置信界限 置信界限
置信界限 置信界限
置信界限 置信界限
置信界限 置信界限
置信界限則稱區間是參數的 置信度為的 置信區間。其中分別稱為 置信下限和 置信上限,置信下限和置信上限統稱 置信界限,稱為 置信度。
 置信界限
置信界限 置信界限
置信界限 置信界限
置信界限 置信界限
置信界限 置信界限
置信界限 置信界限
置信界限 置信界限
置信界限 置信界限
置信界限 置信界限
置信界限 置信界限
置信界限置信區間不同於一般的區間,它是隨機區間。對於樣本的每個觀察值相應確定一個區間。式(1)的意義是,反覆抽樣多次(各次的樣本容量都為n),得到眾多的區間,在這些區間中有的包含參數的真值,有的不包含的真值,當置信度為時,包含真值的約占,不包含真值的僅占;但要注意的是,這裡不說的真值以的機率落入該區間,這是因為真值客觀上是確定值,不是隨機變數。
由於正態隨機變數的廣泛存在,討論正態總體中參數的區間估計有重要的意義 。
置信區間
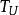 置信界限
置信界限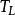 置信界限
置信界限置信區間指包括在置信界限之間的區間。在做區間估計時,首先要確定置信度,即置信機率,然後用有保證的置信度來計算能夠包括母體參數在內的區間稱為置信區間。而置信區間的上限值與下限值就是 置信界限。確定母體參數的置信區間與確定母體參數在某置信區間內的機率是分不開的。所以,確切地說,應稱置信機率為XX值的置信區間。例如,母體平均值的置信區門為(-0.24,5.64),在此區間出現母體平均值的機率為則稱區間(-0.21,5.64) 為母體平均值的95%置信區間。
單側置信區間
 置信界限
置信界限 置信界限
置信界限 置信界限
置信界限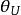 置信界限
置信界限對母體分布函式進行估計時,若對給定的,能找到一個(或),使得
 置信界限
置信界限或
 置信界限
置信界限 置信界限
置信界限 置信界限
置信界限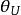 置信界限
置信界限 置信界限
置信界限則稱的區間(或的最小可能值到的區間) 為 單側置信區間。式中稱為置信度。
雙側置信區間
 置信界限
置信界限 置信界限
置信界限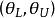 置信界限
置信界限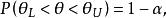 置信界限
置信界限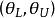 置信界限
置信界限 置信界限
置信界限對母體分布參數進行估計時,若對於給定的,能找到一個區間使得就稱為的 雙側置信區間。
 置信界限
置信界限 置信界限
置信界限 置信界限
置信界限 置信界限
置信界限 置信界限
置信界限 置信界限
置信界限 置信界限
置信界限 置信界限
置信界限 置信界限
置信界限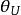 置信界限
置信界限若反覆多次抽樣,當子樣大小不變、每群子樣確定一個區間,每個這樣的區間,要么包含的真值,要么不包含的真值,根據貝努利定理,這樣多的區間中包含真值的約占,不包含真值的僅占左右。例如,若,反覆抽樣1000次,則得到的1000個區間中不包含真值的僅有10個左右。與雙側置信區間對應的是單側置信區間。單側置信區間僅有或其中之一的單側置信界限 。

