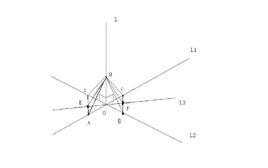
判定定理
判定定理:如果一條直線與平面內兩條相交直線都垂直,那么這條直線與這個平面垂直。
注意關鍵字“相交”,如果是平行直線,則無法判定線面垂直。需要相交的原因見下文。
反證法
設有一直線l與面S上兩條相交直線AB、CD都垂直,則l⊥面S
假設l不垂直於面S,則要么l∥S,要么斜交於S且夾角不等於90。
當l∥S時,則l不可能與AB和CD都垂直。這是因為當l⊥AB時,過l任意作一個平面R與S交於m,則由線面平行的性質可知m∥l
∴m⊥AB
又∵l⊥CD
∴m⊥CD
∴AB∥CD,與已知條件矛盾。
當l斜交S時,過交點在S內作一直線n⊥l,則n和l構成一個新的平面T,且T和S斜交(若T⊥S,則n是兩平面交線。由面面垂直的性質可知l⊥S,與l斜交S矛盾)。
∵l⊥AB
∴AB∥n
∵l⊥CD
∴CD∥n
∴AB∥CD,與已知條件矛盾。
綜上,l⊥S
幾何法
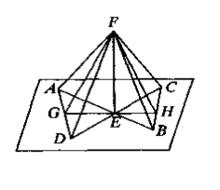 線面垂直
線面垂直如圖,已知l⊥m,l⊥n,m,n⊂α,m∩n=E。求證:EF⊥α
因為平移不改變角度,所以可以通過平移把所有的直線移動到相交於一點的位置來證明。
證明:∵l⊥m,l⊥n
∴在α內所有與m或n平行的直線都與l垂直。
接下來證明那些與m,n不平行的直線也與l垂直。
取m上A,B兩點,取n上C,D兩點,使AE=BE,CE=DE
連線AD,BC,過E作任意一條直線,該直線與AD,BC交點為G,H(稍後將討論GH與AD,BC平行的情況)
取l上異於E的點F,連線FA,FG,FD,FB,FH,FC
∵AE=BE,CE=DE,∠AED=∠BEC
∴△AED≌△BEC(SAS)
∴∠DAE=∠CBE,AD=BC
∵∠AEG=∠BEH
∴△AEG≌△BEH(ASA)
∴AG=BH,GE=HE
∵EF⊥AB,AE=BE
∴FA=FB
同理,FC=FD
∴△FAD≌△FBC(SSS)
∴∠FAG=∠FBH
∴△PAG≌△PBH(SAS)
∴FG=FH
又∵GE=HE
∴FE⊥GH
由GH的任意性可知,EF垂直平面內任意與AD,BC都不平行的直線
當GH∥AD∥BC時,可以連線AC,BD,那么GH必與AC,BD相交
之後證明方法同上,只需要改字母即可。
根據線面垂直的定義,l⊥α
代數法
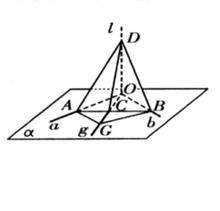 線面垂直
線面垂直如圖,l與α內兩條相交直線a,b都垂直,求證:l⊥α
證明:與a或b平行的直線必垂直l,因此接下來的討論圍繞與a,b不平行的直線進行。
先將a,b,l平移至相交於O點,過O作任意一條直線g,在g上取異於O的點G,過G作GB∥a交b於B,過G作GA∥b交a於A。連線AB,設AB與OG交點為C
∵OA∥GB,OB∥GA
∴四邊形OAGB是平行四邊形
∴C是AB中點
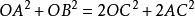 線面垂直
線面垂直由中線定理,
在l上取異於O的點D,連線DA,DB,由中線定理
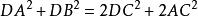 線面垂直
線面垂直兩式相減可得
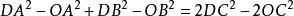 線面垂直
線面垂直又注意到OD⊥OA,OD⊥OB
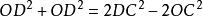 線面垂直
線面垂直∴得
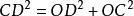 線面垂直
線面垂直即
∴OD⊥OC
由g的任意性可知,l與α內任意直線都垂直
∴l⊥α
向量法
設直線l是與α內相交直線a,b都垂直的直線,求證:l⊥α
證明:設a,b,l的方向向量為 a, b, l
∵a與b相交,即a,b不共線
∴由平面向量基本定理可知,α內任意一個向量 c都可以寫成 c= λ a+ μ b的形式
∵l⊥a,l⊥b
∴ l· a=0, l· b=0
l· c= l·(λ a+ μ b)=λ l·a+ μ l·b=0+0=0
∴ l⊥ c
設c是α內任一直線c的方向向量,則有l⊥c
根據c的任意性,l與α內任一直線都垂直
∴l⊥α
性質定理
性質定理
性質定理1:如果一條直線垂直於一個平面,那么該直線垂直於平面內的所有直線。
性質定理2:經過空間內一點,有且只有一條直線垂直已知平面。
性質定理3:如果在兩條平行直線中,有一條直線垂直於一個平面,那么另一條直線也垂直於這個平面。
性質定理4:垂直於同一平面的兩條直線平行。
推論:空間內如果兩條直線都與第三條直線平行,那么這兩條直線平行。(該推論意味著平行線的傳遞性不僅在平面幾何上,在空間幾何上也成立。)
定理1證明
很容易由線面垂直的定義得到,若不垂直於所有直線,則不可能垂直平面。
定理2證明
已知平面α和一點P,求證過P垂直於α的直線有且只有一條。
當P在平面外時,假設過P有兩條直線m、n都與α垂直,不妨設垂足為M、N。由於m∩n=P,那么m和n確定一個平面β。不難證明α∩β=MN。
∵m⊥α,n⊥α
∴m⊥MN,n⊥MN。這樣一來,在β內就有PM、PN與MN都垂直,與平面內的垂線公理(其實是定理,因為可以依靠歐式幾何的公理證明)矛盾。
類似地可證明當P在平面上時也能推出矛盾。
因此定理2成立。
定理3證明
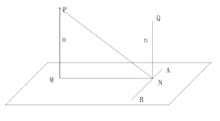 線面垂直
線面垂直已知m∥n,m⊥α,求證n⊥α。
證明:設m∩α=M,n∩α=N。再在m、n上分別另取P、Q。
∵m∥n
∴設m與n確定平面β,且α∩β=MN
過N在α內作AB⊥MN,連線PN。
∵PM⊥α,AB⊂α
∴PM⊥AB
∵PM⊂β,MN⊂β
∴AB⊥β
∵QN⊂β
∴QN⊥AB~~~①
又∵PM⊥α,MN⊂α
∴PM⊥MN
∵PM∥QN
∴QN⊥MN~~~②
∵MN∩AB=N,MN⊂α,AB⊂α
∴QN⊥α
定理4證明
已知m⊥α,n⊥α,求證m∥n
證明:假設m和n不平行,那么它們相交或異面。
當它們相交的時候,設m∩n=P,則m、n確定一個平面
設m⊥α於M,n⊥α於N,連線MN。
則MN在m、n所確定的平面上
易證PM⊥α,MN⊂α
∴PM⊥MN
同理可證PN⊥MN
∵PMN共面,即在該平面內有兩條直線PM、PN與MN都垂直,這與平面內的垂直定理矛盾
∴mn不相交
當它們異面的時候,過N作n‘∥m
∵m⊥α,由定理3可知n’⊥α
又∵n⊥α,n∩n‘=N
即過N有n和n’都與α垂直,這與定理2矛盾
∴mn不異面
∴m∥n
推論證明
已知空間內有三條直線a、b、c,且三條直線不同在一個平面內。若a∥b,b∥c,求證a∥c。
幾何法證明:在a上任意取一點A,由於兩條平行直線確定一個平面,因此在a和b所確定的平面內,過A作b的垂線AB,垂足為B。同理,在b和c所確定的平面內,過B作c的垂線BC,垂足為C。連線AC。
∵b∥c,BC⊥c
∴BC⊥b
∵AB⊥b
∴b⊥平面ABC(判定定理)
∵a∥b
∴a⊥平面ABC(性質定理3)
∵c∥b
∴c⊥平面ABC(性質定理3)
∴a∥c(性質定理4)
向量法證明:設a的方向向量為 a,b的方向向量為 b,c的方向向量為 c,其中 a、 b、 c都是非零向量。
∵a∥b
∴ a∥ b
由共線向量基本定理可知存在一個唯一實數λ(λ≠0)使得a=λb
同理,存在一個唯一實數μ(μ≠0)使得 b=μ c
∴ a=λ*(μ c)=(λ*μ) c
∴ a∥ c
∴a∥c
反證法證明:假設a和c不平行,要么它們相交,要么它們異面。
若a和c相交於P,則它們確定一個平面α。又設a和b確定的平面為β。
明顯,α∩β=a
∵a∩c=P
∴c不在β上。這是因為由於兩個相交平面只有一條交線,這條交線就是a。而c⊂α,如果c⊂β,說明c和a重合,這與它們相交矛盾。
∵a∥b,P∈a
∴P∉b
由異面直線的判定定理( 經過平面外一點與平面內一點的直線,與平面內不經過該點的直線互為異面直線)可知b和c互為異面直線(只要取c上其他一點Q即可,Q必定不在β上,否則P、Q都在β上那么c就在β上,與前文所述矛盾)。但這與條件中b∥c矛盾,因此一開始的假設不成立,a和c不相交。
若a和c異面,則根據異面直線所成角的定義,平行於異面直線其中一條的直線與異面直線的另一條所成角等於原來的異面直線所成角
∵a∥b
∴a與c所成角等於b與c所成角
但b∥c,即b與c所成角為0°
∴a與c所成角為0°,這和異面直線所成角的範圍(0°,90°]相矛盾
∴a和c不異面
∴a∥c
線面垂直
由性質定理2可知,過空間內一點(無論是否在已知平面上),有且只有一條直線與平面垂直。下面就討論如何作出這條唯一的直線。(下面的作法利用到的是過一點作已知直線的垂線/平行線,這是尺規作圖中最基本的例子之一,故不再詳細介紹。)
點在平面外
設點P是平面α外的任意一點,求作一條直線PQ使PQ⊥α。
作法:
①在α內任意作一條直線l,並過P作PA⊥l,垂足為A。
此時,若PA⊥α,則所需PQ已作出;若不是這樣,
②在α內過A作m⊥l。
③過P作PQ⊥m,垂足為Q,則PQ是所求直線。
證明:
由作法可知,l⊥PA,l⊥QA
∵PA∩QA=A
∴l⊥平面PQA
∴PQ⊥l
又∵PQ⊥m,且m∩l=A,m⊂α,l⊂α
∴PQ⊥α
點在平面內
設點P是平面α內的任意一點,求作一條直線PQ使PQ⊥α。
作法:
①過平面外一點A作AB⊥α,作法見上。
②過P作PQ∥AB,PQ是所求直線。
證明:
由性質定理3可知,若作出了AB⊥α,PQ∥AB,那麼PQ⊥α。