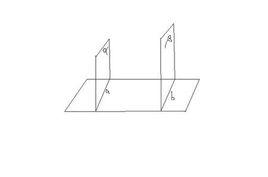
判定定理
定理
一個平面過另一平面的垂線,則這兩個平面相互垂直。
幾何描述:若a⊥β,a⊂α,則α⊥β
證明:任意兩個平面關係為相交或平行,設a⊥β,垂足為P,那么P∈β
∵a⊂α,P∈a
∴P∈α
即α和β有公共點P,因此α與β相交。
設α∩β=b,∵P是α和β的公共點
∴P∈b
過P在β內作c⊥b
∵b⊂β,a⊥β
∴a⊥b,垂足為P
又c⊥b,垂足為P
∴∠aPc是二面角α-b-β的平面角
∵c⊂β
∴a⊥c,即∠aPc=90°
根據面面垂直的定義,α⊥β
推論1
如果一個平面的垂線平行於另一個平面,那么這兩個平面互相垂直。
已知α⊥a,a∥β,求證α⊥β
證明:過a任意作一個平面γ與β相交,設交線為c
∵a∥β
∴a∥c(線面平行的性質定理)
∵a⊥α
∴c⊥α(線面垂直的性質定理)
∵c⊂β
∴β⊥α(定理1)
推論2
如果兩個平面的垂線互相垂直,那么這兩個平面互相垂直。(可理解為法向量垂直的平面互相垂直)
證明:設有a⊥α,b⊥β,且a⊥b
則根據線面平行的判定定理,有a∥β
∵a⊥α
∴α⊥β(推論1)
這些定理和推論都是向量法解題的基礎,例如向量法解得一個平面的法向量與另一個平面平行,那么這兩個平面就垂直。
性質定理
定理1
如果兩個平面相互垂直,那么在一個平面內垂直於它們交線的直線垂直於另一個平面。
已知:α⊥β,α∩β=l,O∈l,OP⊥l,OP⊂α。
求證:OP⊥β。
證明:過O在β內作OQ⊥l,則由二面角知識可知∠POQ是二面角α-l-β的平面角。
∵α⊥β
∴∠POQ=90°,即OP⊥OQ
∵OP⊥l,l∩OQ=O,l⊂β,OQ⊂β
∴OP⊥β
定理2
如果兩個平面相互垂直,那么經過第一個平面內的一點作垂直於第二個平面的直線在第一個平面內。
已知α⊥β,A∈α,AB⊥β。求證:AB⊂α
證明:假設AB不在α內,則AB與α只有一個交點A。(因為不可能直線的一部分在平面內而另一部分在平面外,即直線的兩點在面上則直線就在面上)
當A在α和β的交線外時,則B是垂足
∵AB⊥β於B
∴B∈β
設α∩β=MN,過B在β內作BC⊥MN,由定理1可知BC⊥α
連線AC
∵AC⊂α
∴AC⊥BC
但AB⊥β,BC⊂β
∴AB⊥BC
即在平面ABC上,過一點A有AB、AC同時垂直BC,與垂直定理矛盾。
當A在α和β的交線上時,A是垂足。
設α∩β=MN,在α內作AC⊥MN,由定理1可知AC⊥β
但AB⊥β,即過A有兩條直線AB、AC與β垂直,這和線面垂直的性質定理矛盾
∴假設不成立,AB⊂α
定理3
如果兩個相交平面都垂直於第三個平面,那么它們的交線垂直於第三個平面。
已知:α⊥γ,β⊥γ,α∩β=l。求證:l⊥γ
證明:設α∩γ=a,β∩γ=b
∵a∩b=l
∴a與b相交
設a∩b=P,則P∈l
若l與γ不垂直,那么在α內過P作PA⊥a,由定理1可知PA⊥γ
同理,在β內作PB⊥b,就有PB⊥γ
於是過P有兩條直線與γ垂直,與線面垂直的性質定理矛盾。
∴假設不成立,l⊥γ
推論
三個兩兩垂直的平面的交線兩兩垂直。
已知:α⊥β,β⊥γ,γ⊥α,且α∩β=a,β∩γ=b,γ∩α=c
求證:a⊥b,a⊥c,b⊥c
證明:∵α∩β=a,α⊥γ,β⊥γ
∴a⊥γ(定理3)
∵b⊂γ,c⊂γ
∴a⊥b,a⊥c
同理可證b⊥c
定理4
如果兩個平面互相垂直,那么一個平面的垂線與另一個平面平行。(判定定理推論1的逆定理)
已知α⊥β,a⊥β,a∉α。求證a∥α
證明:假設a與α不平行,那么他們相交。設交點是A
又設a⊥β,垂足為B。α∩β=l
在α內作AC⊥l,由定理1可知AC⊥β
則過點A有AB、AC與β垂直,與線面垂直的性質定理矛盾
∴a∥α
推論
如果兩個平面互相垂直,那么分別垂直於這兩個平面的兩條垂線也互相垂直。(判定定理推論2的逆定理)
可以根據定理4先證明一個平面的垂線平行於另一個平面,再根據線面平行的性質證明這條直線與另一個平面的垂線垂直。