概述
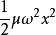 線性諧振子
線性諧振子 線性諧振子
線性諧振子 線性諧振子
線性諧振子 線性諧振子
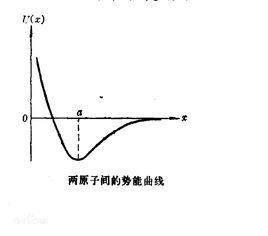
線性諧振子如果在一維空間內運動的粒子勢能為 , 是常量,則這種體系就稱為線性諧振子。這個問題的重要性在於許多體系都可以近似地看作是線性諧振子。例如,雙原子分子中兩原子之間的勢能 是兩原子間距離 的函式,其形狀如圖1所示。
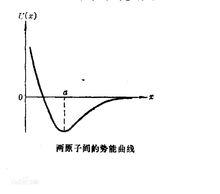 圖1
圖1 線性諧振子
線性諧振子 線性諧振子
線性諧振子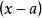 線性諧振子
線性諧振子 線性諧振子
線性諧振子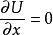 線性諧振子
線性諧振子 線性諧振子
線性諧振子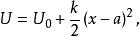 線性諧振子
線性諧振子 線性諧振子
線性諧振子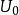 線性諧振子
線性諧振子在 處,勢能有一極小值,這是一個穩定平衡點。在這點附近, 可以展成 的冪級數,又因為在 處, ,所以 可以近似地寫成:式中和都是常量。這正是線性諧振子的勢能。一般說來,任何一個體系在穩定平衡點附近都可以近似地用線性諧振子來表示。
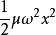 線性諧振子
線性諧振子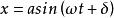 線性諧振子
線性諧振子 線性諧振子
線性諧振子 線性諧振子
線性諧振子在經典力學中,線性諧振子的運動是簡諧運動。勢能為的線性諧振子,其坐標與時間的關係是,是振幅,是初相。
基本原理
 線性諧振子
線性諧振子 線性諧振子
線性諧振子 線性諧振子
線性諧振子線性諧振子是物理學中一個重要的模型,許多在平衡點附近振動的物理問題都可簡化為線性諧振運動。在經典理論中質量為 、距離平衡點位置為 、振動頻率為 的線性諧振子,其總能量為:
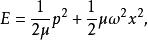 線性諧振子
線性諧振子第一項為其動能,第二項為其勢能。反之,能量具有上述形式的運動質點就稱為線性諧振子。如果粒子的哈密頓量具有形式:
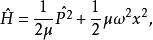 線性諧振子
線性諧振子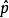 線性諧振子
線性諧振子 線性諧振子
線性諧振子其中 是粒子的動量算符, 是坐標算符,則算符這樣的微觀粒子為量子力學中的線性諧振子。通過求解它的能量本徵值方程得到其能量為:
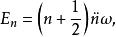 線性諧振子
線性諧振子 線性諧振子
線性諧振子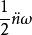 線性諧振子
線性諧振子其中 =0,1,2,… 。這表明線性諧振子的能量是一系列不連續的值,其中最低的能量是 ,稱為零點能。這兩點同經典諧振子截然不同。