線性自由能關係
正文
有機反應中速率常數和平衡常數與分子中取代基效應之間的定量關係。這是一類經驗的、近似的定量關係。著名的哈米特方程、塔夫脫方程、布侖斯惕酸鹼催化定律和斯溫方程都屬於這種關係。哈米特方程 1937年美國的L.P.哈米特研究了許多系列芳族化合物的反應速率常數和平衡常數與取代基之間的定量關係。在這些系列化合物中,每個化合物都有一個相同的反應中心,但在該反應中心的間位和對位上,有不同的取代基。哈米特發現,這些化合物中任一個化合物的反應速率常數或平衡常數可用方程 (1)和(1′)近似算得:
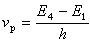 (1)
(1)
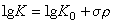 (1′)
(1′)
K、k與ΔF°、ΔF≠的關係可用方程(2)、(3)表示:
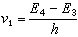 (2)
(2)
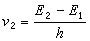 (3)
(3)
方程(1)、(1′)可分別寫成方程(4)、(4′):
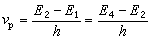 (4)
(4)
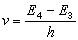 (4′)
(4′)
塔夫脫方程 50年代R.W.塔夫脫髮現:當反應中心不是共軛體系的一個部分,取代基與反應中心之間的立體效應的程度在反應過程中沒有明顯變化時,則脂肪族化合物的活性與結構之間的定量關係可以用與哈米特方程相似的方程(5)來描述:
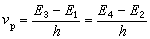 (5)
(5)
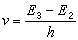 (6)
(6)
為取代的乙酸乙酯的水解速率常數;k0為乙酸乙酯的水解速率常數;(k/k0)B為鹼催化 (見酸鹼催化作用)的速率常數之比;(k/k0)A為酸催化的速率常數之比;ρ*為反應常數。同樣,方程(5)可寫成方程(7):
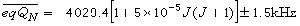 (7)
(7)
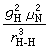 (8)
(8)
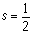 (9)
(9)
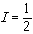 (10)
(10)
斯溫方程 C.G.斯溫定量地描述了親核取代反應速率常數與作用物、進攻試劑和溶劑之間的關係:
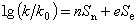 (11)
(11)
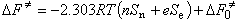 (12)
(12)
有機化學中 BEP原理是反應活化能(ΔE)與反應熱(ΔH)之間的一種近似的線性關係(13),實質上也可歸屬於線性自由能關係:
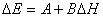 (13)
(13)
參考書目
E.S.Gould, Mechanism and Structure in Organic Chemistry, Holt, New York, 1960.
